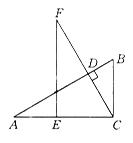
如图1－29所示，在△ABC中，∠ACB＝90°，CD⊥AB于点D，点E在AC上．CE ＝BC，过点E作AC的垂线，交CD的延长线于点F，求证AB＝FC．
名校课堂系列答案科目：初中数学 来源： 题型：
下列各式中，正确的是（ ）
A、sin200+sin300=sin500； B、sin600=2sin300；
C、tan200﹒t
an700=1； D、cos300＜cos600；
查看答案和解析>>
科目：初中数学 来源： 题型：
具备下列条件的两个三角形可以
判定它们全等的是 （ ）
A．一边和这边上的高对应相等 B．两边和第三边上的高对应相等
C．两边和其中一边的对角对应相等 D．两个直角三角形中的斜边对应相等
查看答案和解析>>
科目：初中数学 来源： 题型：
三个牧童A，B，C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时，他们所需走的最大距离（看守点到本区域内最远处的距离）相等．按照这一原则，他们先设计了一种如图1－49（1）所示的划分方案，把正方形牧场分成三块相等的矩形，大家分头守在这三个矩形的中心（对角线交点），看守自己的一块牧场．过了一段时间，牧童B和牧童C又分别提出了新的
划分方案．牧童B的划分方案如图1－49（2）所示，三块矩形的面积相等，牧童的位置在三个小矩形的中心．牧童C的划分方案如图1－49（3）所示，把正方形的牧场分成三块矩形，牧童的位置在三个小矩形的中心，并保证在有情况时三个要所需走的最大距离相等．
（1）牧童B的划分方案中，牧童 （填“A”“B”或“C”）在有情况时所需走的最大距离较远．
（2）牧童C的划分方案是否符合他们商量的划分原则?为什么?（提示：在计算
时可取正方形边长为2）
查看答案和解析>>
科目：初中数学 来源： 题型：
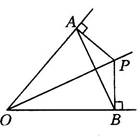
如图1—104所示，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B，下列结论不一定成立的是 （ ）
A．PA=PB B．PO平分∠APB
C．OA=OB D．AB垂直平分OP
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＝90°，∴∠FEC＝∠ACB＝90°，∴∠F+∠ECF＝90°．又∵CD⊥AB于点D，∴∠A+∠ECF＝90°，∴∠A＝∠F．在△ABC和△FCE中，∠A＝∠F，∠ACB＝∠FEC，BC＝CE，∴△ABC≌△FCE，∴AB＝FC．
）
分 成了两个等腰三角形，