
����Ŀ�����壺��ͼ1��������ABC�У���E��F�ֱ�����AB��AC�ϣ�����EF����AE��CF�����EFΪ�õ��������ε�����ߣ�
��1����ͼ1��EF�ǵ�����ABC������ߣ���EF��AB��AB��AC��5��AE ��2���������EF�ij���
��2����ͼ2��������ֱ�ǡ�DEF��ֱ�Ƕ���Dǡ��Ϊ����ֱ�ǡ�ABC�ױ�BC�ϵ��е㣬�ҵ�E��F�ֱ���AB��AC�ϣ���֤��EFΪ������ABC������ߣ�
��3����ͼ3���߳�Ϊ6�ĵȱ������Ρ�AOC�ı�OC��X���غϣ�EF�Ǹõȱ������ε�����ߣ�F�������Ϊ��5��![]() ���������E������(����Ҫ���������ֱ��Ӧ�ý��ۣ���ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ����)
���������E������(����Ҫ���������ֱ��Ӧ�ý��ۣ���ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ����)
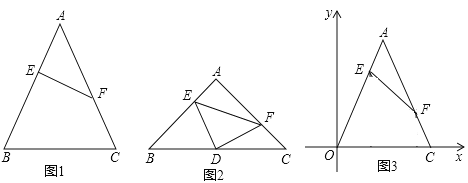
���𰸡���1��![]() ��2�������� ��3��E��2��
��2�������� ��3��E��2��![]() ��
��
��������
��1��������ߵ����ʿ����CF��AE�������������AF����Rt��AEF�У��ɹ��ɶ��������EF�ij���
��2������AD����֤����EDA�ա�FDC�������AE=CF����֤�ý��ۣ�
��3����E��F�ֱ���EG��OC��G , FH��OC��H���ɹ��ɶ����ɵ�FC![]() ���������֪AE=2������OEG�У��ֱ����OG��EG���ɵõ�E������.
���������֪AE=2������OEG�У��ֱ����OG��EG���ɵõ�E������.
�⣺
��1����EF�ǵ�����ABC������ߣ�
��CF=AE=2����AB=AC=5��
��AF=3��
��EF��AB��
��EF=![]() =
=![]() ��
��
��2������AD���ڵ���Rt��ABC�У���DΪ�ױ����е㣬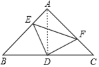
��AD=CD�ҡ�ADC=90�㣬
�֡�DE=DF�ҡ�EDF=90�㣬
���EDA=90��-��ADF=��FDC��
�ڡ�EDA�͡�FDC����
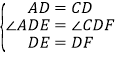 ,
,
���EDA�ա�FDC��SAS����
��AE=CF��
��EFΪ������ABC������ߣ�
(3)��E��F�ֱ���EG��OC��G , FH��OC��H��
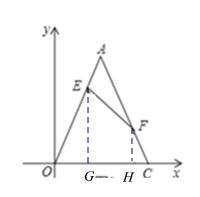
��F���������5��![]() ����
����
��FH=![]() ,OH=5��
,OH=5��
��HC=OC-OH=6-5=1,
��Rt��FHC��FC=![]() ,
,
��AE=FC=2,
��OE=OA-AE=6-2=4,
����FH��OC����AOC=60�㣬
����OEG=30����
��OG=![]() OE=2,( ��ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ��)
OE=2,( ��ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ��)
��EG=![]() =
=![]() =
=![]() ,
,
��E��2��![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����������ֱ��Ϊ7cm��Բ���ι�ͷ�У��轫��Ģ����ͷ���������ڹ�ͷ���森Ϊ�˻�ýϼ��Ӿ�Ч���������ڹ�ͷ�в������γɵĻ��Ķ���Ϊ90�㣬��Ģ����ͷ�������ij���Ϊ�� �� 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.7��cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʡ�����������ʡ��ũ�������������ͥ�����ͬʱ��Ҳһ���̶�Ӱ������Ů�Ĺ����ͽ�����ȱ�ٹ����ͽ��������ض�ͯ��ѧϰ����������״���������������֣���Ϊ����ע�Ľ��㣮��ʡ��ز��ž����ض�ͯѧϰ����������״����������е��飬���γ��������˸�ʡij�ز������ض�ͯ����������ֵ���������࣬��A�ࣺ�������������B�ࣻ��������⣻C�ࣺ�н�Ϊ�������⣻D�ࣺ���ر��������⣮ͨ�����飬�õ�����������������ͳ��ͼ�������ͼ�е���Ϣ�����������⣮ 
��1�������������������У�������˶�����ѧ�����ض�ͯ��
��2������ͳ��ͼ��C����ռ��Բ�Ľ����㣻��ε�����ΪD������ض�ͯ���ˣ�
��3��������Ƹ���20000�����ض�ͯ�У����ֽ�Ϊ�������⼰���ϵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ı���ABCD�У���DAB���Խ���ACƽ�֣���AC2=ABAD�����dzƸ��ı���Ϊ���ɷ��ı��Ρ�����DAB��Ϊ���ɷֽǡ���
��1����ͼ2�����ı���ABCD�У���DAB=60�㣬ACƽ�֡�DAB���ҡ�BCD=150�㣬��֤���ı���ABCDΪ���ɷ��ı��Ρ���
��2����ͼ3���ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ��������DCB=��DAB�������DAB�Ķ�����
��3�������ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ�����AC=4�����DAB������������ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD=10��AB=4����Q��BC���е㣬��P��AD�����˶�������BPQ�ǵ���������ʱ��AP�ij�Ϊ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�3����Ϊ����Ӳμ�ѧУ���еġ���ˮ���Ρ�֪ʶ�������ڰ���ѡȡ��������ѧ�����ֳ�������ͬ�ļס������飬�������ĴΡ���ˮ���Ρ�ģ�⾺�����ɼ�����������������ʷֱ���Ƴ���ͼͳ��ͼ�� 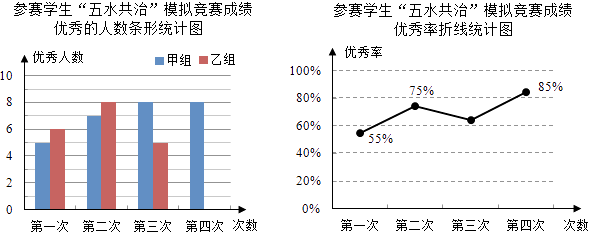
����ͳ��ͼ������������⣺
��1�������γɼ����������Ƕ��٣���������ͳ��ͼ����������
��2������ü���ɼ�����������ƽ���� ![]() =7������
=7������ ![]() =1.5����ͨ������˵������һ��ɼ�������������ȶ���
=1.5����ͨ������˵������һ��ɼ�������������ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������н�����ͼ��ֱ������ϵ����������A��O��B��λ����ͼ�����Ƿֱ��ǣ���1��1������0��0���ͣ�1��0���� 
��1����ͼ2����������C��ʹA��O��B��C�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ�����ͼ�л�����ͼ�εĶԳ��
��2�����������λ������һ������P��ʹA��O��B��P�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ���ֱ��д������P��λ�õ����꣮��д��2�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����50λѧ����ÿλѧ������һ����ţ���50�ű���ѧ����ţ���1�ŵ�50�ţ��Ŀ�Ƭ������Ų�ͬ����������ͬ������˳���������У����������ȡ1�ſ�Ƭ��
��1��������У���20�ı������У�20��40��������20���У�1��2��4��5��10��Ϊ�˲��ظ�������20ֻ��һ�Σ�����ȡ���Ŀ�Ƭ�������20�ı�����������20�ĸ��ʣ�
��2�����涨��ȡ���Ŀ�Ƭ�������k��k������1��k��50�����������������k�ı�����������k�����ظ���������ѧ���ܲμ�ij������һ�涨�Ƿ�ƽ����˵�����ɣ�
��3���������һ���涨���ܹ�ƽ��ѡ��10λѧ���μ�ij������˵����Ĺ涨�Ƿ���Ҫ��ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������������������ע���ȵ㻰���Ϊ���ѡ����������������������������࣮�������һ����������������ݣ����Ƶ�ͳ��ͼ�����£� 
����������Ϣ����������⣺
��1�����ι������ˣ����ڴ���ϲ�ȫ����ͳ��ͼ�������Ӧ���ݣ�
��2����������Լ��900���˿ڣ�����������ע�������������ԼΪ�������ˣ�
��3������ε����У�ij��λ���мס��ҡ��������������ע�������⣬�������������������ȡ���˽�����̸�����ȡ������ǡ���Ǽ��ҵĸ��ʣ�����״ͼ���б�˵������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com