
分析 (1)根据加减消元法先消去x,求出y,再代入计算即可求解;
(2)根据加减消元法先消去y,求出x,再代入计算即可求解;
(3)根据加减消元法先消去y,求出x,再代入计算即可求解;
(4)先三式相加求得x+y+z的值,再分别与各式相减即可求解.
解答 解:(1)$\left\{\begin{array}{l}{x+3y=2①}\\{x+2y=1②}\end{array}\right.$,
①-②得y=1,
把y=1代入②得x+2=1,解得x=-1.
故方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$.
(2)$\left\{\begin{array}{l}{2x-3y=7①}\\{3x+4y=2②}\end{array}\right.$,
①×4+②×3得17x=34,解得x=2,
把x=2代入②得6+4y=2,解得y=-1.
故方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
(3)$\left\{\begin{array}{l}{5x+\frac{1}{4}y=11①}\\{6x+0.25y=13②}\end{array}\right.$,
②-①得x=2,
把x=2代入②得12+0.25y=13,解得y=4.
故方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$.
(4)$\left\{\begin{array}{l}{x+y=16①}\\{y+z=12②}\\{z+x=10③}\end{array}\right.$,
①+②+③得2(x+y+z)=38,解得x+y+z=19④,
④-①得z=3,
④-②得x=7,
④-③得y=9.
故方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=9}\\{z=3}\end{array}\right.$.
点评 考查了解二元一次方程组,关键是熟练掌握代入法和加减法解二元一次方程组的一般步骤.同时考查了解三元一次方程组,解三元一次方程组的一般步骤:①首先利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组.②然后解这个二元一次方程组,求出这两个未知数的值.③再把求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个关于第三个未知数的一元一次方程.④解这个一元一次方程,求出第三个未知数的值.⑤最后将求得的三个未知数的值用“{”合写在一起即可.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:选择题
| A. | 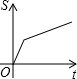 | B. | 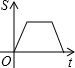 | C. | 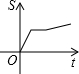 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
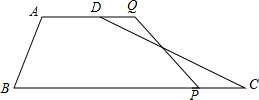 如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,$\sqrt{2}$,4 | B. | 4,5,6 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 3,4,5 | D. | 6,8,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
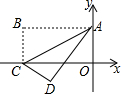 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )| A. | (-$\frac{12}{5}$,-$\frac{6}{5}$) | B. | (-$\frac{12}{5}$,-$\frac{8}{5}$) | C. | ($\frac{12}{5}$,-$\frac{6}{5}$) | D. | ($\frac{12}{5}$,-$\frac{8}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com