
 在矩形ABCD中,AB=6,BC=8,AC,BD相交于O,P是边BC上一点,AP与BD交于点M,DP与AC交于点N.
在矩形ABCD中,AB=6,BC=8,AC,BD相交于O,P是边BC上一点,AP与BD交于点M,DP与AC交于点N.分析 由矩形的性质得出AD=BC,AD∥BC,由平行线得出AM:PM=AD:BP,由中点的定义得出AM:PM=2:1,①正确;
②不正确;作MG⊥BC于G,则MG∥AB,得出△PMG∽△PAB,求出MG=$\frac{1}{3}$AB=2,得出四边形OMPN的面积=△BOC的面积-△MBP的面积-△NCP的面积=4,得出②不正确;
求出图中阴影部分的总面积=矩形ABCD的面积-图中空白部分的面积=28,③正确;
④错误;由P在B时,阴影部分的面积=$\frac{1}{2}$×6×8=24≠28,得出④不正确;即可得出结论.
解答 解:①正确;
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,AD=BC,AD∥BC,
∴AM:PM=AD:BP,
∵点P为BC的中点,
∴BP=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴AM:PM=2:1;
②不正确;作MG⊥BC于G,如图所示: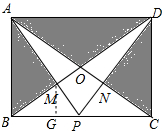
则MG∥AB,
∴△PMG∽△PAB,
∴MG:AB=PM:PA=1:3,
∴MG=$\frac{1}{3}$AB=2,
∴四边形OMPN的面积=△BOC的面积-△MBP的面积-△NCP的面积=$\frac{1}{4}$×8×6-$\frac{1}{2}$×4×2-$\frac{1}{2}$×4×2=4;③正确;
∵图中空白部分的面积=△DBP的面积+△ACP的面积-四边形OMPN的面积=$\frac{1}{2}$×4×6+$\frac{1}{2}$×4×6-4=20,
∴图中阴影部分的总面积=矩形ABCD的面积-图中空白部分的面积=8×6-20=28;④错误;
∵P在B时,阴影部分的面积=$\frac{1}{2}$×6×8=24≠28;
正确的有①③;
故答案为:①③.
点评 本题考查了矩形的性质、相似三角形的判定与性质、三角形以及矩形面积的计算等知识;本题综合性强,有一定难度,通过作辅助线是解决问题②的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
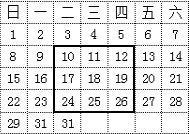 如图是2013年12月的日历表,请你仔细观察长方形框出的9个日期,如果将长方形四个角落的日期分别记为a,b,c,d,那么用一个等式表示a,b,c,d之间的数量关系,可以为a+d=b+c(写出一个即可).
如图是2013年12月的日历表,请你仔细观察长方形框出的9个日期,如果将长方形四个角落的日期分别记为a,b,c,d,那么用一个等式表示a,b,c,d之间的数量关系,可以为a+d=b+c(写出一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
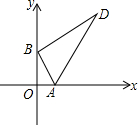 Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最大值和最小值的乘积为48.
Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最大值和最小值的乘积为48.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
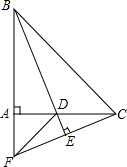 已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.
已知:如图,在等腰直角△ABC中,∠BAC=90°,BD平分∠ABC,交AC于点D,过C作CE⊥BD,交BD的延长线于点E,交BA的延长线于点F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,校园内有两棵树,相距8米,一棵树树高AB=13米,另一棵树高CD=7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
如图,校园内有两棵树,相距8米,一棵树树高AB=13米,另一棵树高CD=7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com