
已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m-5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90º?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
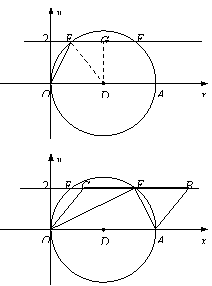 解:(1)由题意,知:BC∥OA.以OA为直径作⊙D,与直
解:(1)由题意,知:BC∥OA.以OA为直径作⊙D,与直
线BC分别交于点E、F,则∠OEA=∠OFA=90º.
作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,
EG=GF,∴ EG=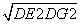 =1.5,
=1.5,
∴点E(1,2),点F(4,2).
∴当 即1≤m≤9时,边BC上总存在这样的点P,
即1≤m≤9时,边BC上总存在这样的点P,
使∠OPA=90º.
(2)∵BC=5=OA,BC∥OA,∴四边形OABC是平行四边形.
当Q在边BC上时,∠OQA =180º-∠QOA-∠QAO
=180º- (∠COA+∠OAB)=90º,∴点Q只能是点E或点F
(∠COA+∠OAB)=90º,∴点Q只能是点E或点F .
.
当Q在F点时,∵OF、AF分别是∠AOC与∠OAB的平分
线,BC∥OA,∴∠CFO=∠FOA=∠FOC,∠BFA=∠FAO=
∠FAB,∴CF=OC,BF=AB,∵OC=AB,∴F是BC的中
点.∵F点为 (4,2),∴此时m的值为6.5.
当Q在E点时,同理可求得此时m的值为3.5.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
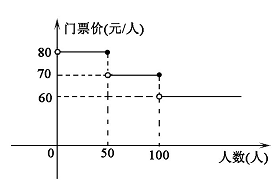
我市某风景区门票价格如图所示黄冈赤壁旅游公司有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120 人,乙团队人数不超过50 人.设甲团队人数为x 人,如果甲、乙两团队分别购买门票,两团队门票款之和为W 元.
(1)求W 关于x 的函数关系式,并写出自变量x 的取值范围;
(2)若甲团队人数不超过100 人,请说明甲、乙两团队联合购票比分别购票最多可节约多少钱;
(3“) 五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50 人时,门票价格不变;人数超过50 人但不超过100 人时,每张门票降价a 元;人数超过100 人时,每张门票降价2a 元.在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,最多可节约3400 元,求a 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
某种蔬菜按品质分成三个等级销售,销售情况如下表:
| 等级 | 单价(元/千克) | 销售量(千克) |
| 一等 | 5.0 | 20 |
| 二等 | 4.5 | 40 |
| 三等 | 4.0 | 40 |
则售出蔬菜的平均单价为 元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地后正面朝上;
③任取两个正整数,其和大于1;④长分别为3、5、9厘米的三条线段能围成一个三角形.
其中确定事件的个数是( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A队的积分至少要( )分才能保证一定出线.【注:单循环比赛就是小组内的每一个队都要和其他队赛一场】
A.7 B.6 C.4 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
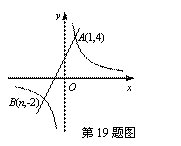
如图,已知反比例函数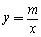 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com