
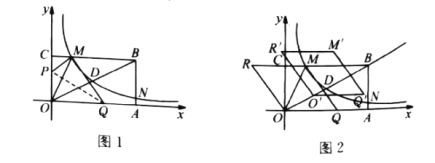
����Ŀ����ͼ������OABC�Ķ���A��C��x��y���������ϣ�����������![]() ��OB���е�D����BC��AB����M,N������֪D(m,2),N(8,n)��
��OB���е�D����BC��AB����M,N������֪D(m,2),N(8,n)��
��1�����������Ľ���ʽ��
��2����������һ���۵���ʹ��O���M�غϣ��ۺ�ΪPQ�����P�����ꣻ
��3����ͼ2������![]() ��OM�����ۣ��õ�����OQMR����������������OB��ÿ��
��OM�����ۣ��õ�����OQMR����������������OB��ÿ��![]() ����λ����ƽ��t�룮
����λ����ƽ��t�룮
�� ��t�Ĵ���ʽ��ʾ![]() ��
��![]() �����ꣻ
�����ꣻ
�� Ҫʹ������ʼ���뷴��������ͼ���н��㣬��t��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ����3����
����3����![]() ��
��![]() ����
���� ![]()
��������
��1���������OA=8����ΪDΪOB���е㣬�ó�D��4��2�������뷴���������Ľ���ʽ�ɵã�
��2�����M������꣬�����ù��ɶ������OP�ij����ɵõ�P���ꣻ
��3���ٹ���O����O��T��x�ᣬ����ΪT���ɵ���OO��T�ס�OBA�������ɱ�ʾ![]() �����꣬���ù��ɶ������CR���ɱ�ʾ
�����꣬���ù��ɶ������CR���ɱ�ʾ![]() �����ꣻ
�����ꣻ
�ڰ�R����2t-3��t+4�����뷴���������Ľ���ʽ��ɣ�
�⣺��1����N��8��n�����ı���OABC�Ǿ��Σ�
��OA=8��
��DΪOB���е㣬
��D��4��2����
��2=![]() ����k=8��
����k=8��
��y=![]() ��
��
��2����D��4��2����
���M������Ϊ4��
��4=![]() ����x=2��
����x=2��
��M��2��4����
��OP=x����MP=x��CP=4-x��CM=2���ɹ��ɶ����ã���4-x��2+22=x2��
��ã�x=![]() ����OP=
����OP=![]() ��
��
��P��0��![]() ����
����
��3���ٹ���O����O��T��x�ᣬ����ΪT��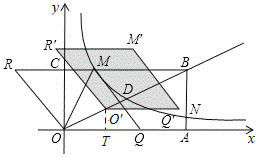
�ɵá�OO��T�ס�OBA��
��![]() ��
��
��![]() =
=![]() ��
��
��OO��=![]() ��
��
��OT=2t��O��T=t��
��O����2t��t����
��CR=x����OR=RM=x+2��
��x2+42=��x+2��2�����x=3����CR=3��
��R����2t-3��t+4����
�ڡ�R����2t-3��t+4����
��������ã�t+4=![]() ��
��
����ã�2t2+5t-20=0��
��ã�![]() ��
��![]() ����ȥ����
����ȥ����
![]()


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD=6��AB��BC��AD��CD����BAD=60������M��N�ֱ���AB��AD���ϣ���AM��MB=AN��ND=1��2����tan��MCN=

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
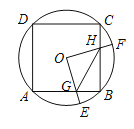
����Ŀ����ͼ���߳�Ϊ4��������ABCD�ڽ�����O����E��![]() �ϵ�һ���㣨�����A��B�غϣ�����F��
�ϵ�һ���㣨�����A��B�غϣ�����F��![]() �ϵ�һ��������OE��OF���ֱ��뽻AB��BC�ڵ�G��H������EOF��90��������GH�������н�����
�ϵ�һ��������OE��OF���ֱ��뽻AB��BC�ڵ�G��H������EOF��90��������GH�������н�����
��![]() ���ڡ�OGH�ǵ���ֱ�������Σ����ı���OGBH��������ŵ�Eλ�õı仯���仯���ܡ�GBH�ܳ�����СֵΪ
���ڡ�OGH�ǵ���ֱ�������Σ����ı���OGBH��������ŵ�Eλ�õı仯���仯���ܡ�GBH�ܳ�����СֵΪ![]() .������ȷ����____________����������Ϊ��ȷ���۵���Ŷ����ϣ�
.������ȷ����____________����������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
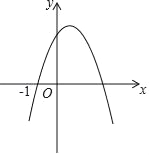
����Ŀ����ͼ������y=ax2+bx+c��ͼ����㣨��1��0���ͣ�m��0������˼�������жϣ���abc��0����4a+c��2b����![]() =1��
=1��![]() ����am2+��2a+b��m+a+b+c��0����|am+a|=
����am2+��2a+b��m+a+b+c��0����|am+a|=![]() ��ȷ���ǣ�������
��ȷ���ǣ�������
A. �٢ۢ� B. �٢ڢۢܢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У������²�����ͼ������AΪԲ�ģ����ⳤΪ�뾶�������ֱ�AB��AD�ڵ�M��N�����ֱ���M��NΪԲ�ģ��Դ���![]() MN��Ϊ�뾶�����������ཻ�ڵ�P����������AP������CD�ڵ�Q����DC��3QC��BC��6����ƽ���ı���ABCD�ܳ�Ϊ_____��
MN��Ϊ�뾶�����������ཻ�ڵ�P����������AP������CD�ڵ�Q����DC��3QC��BC��6����ƽ���ı���ABCD�ܳ�Ϊ_____��
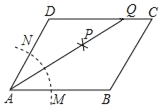
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1��kx+b��ͼ���뷴��������y2��![]() ��ͼ���ڵ�A����3��2����B��n����6�����㣮
��ͼ���ڵ�A����3��2����B��n����6�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����AOB�������
��3����ֱ��д��y1��y2ʱx�ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿѧ�����������ʣ������������Ź涨ѧ��ÿ�컧����ƽ��ʱ�䲻����1Сʱ��Ϊ�˽�ѧ���μӻ�����������Բ���ѧ���μӻ�����ʱ����г������飬�������������Ƴ���ͼ��������������ͳ�ƣ��������ͼ���ṩ����Ϣ����������⣺


��1������ε����й������˶�����ѧ����
��2����7����ʱ��Ϊ0.5Сʱ��������������Ƶ���ֲ�ֱ��ͼ��
��3�����ʾ����ʱ��Ϊ2Сʱ������Բ�ĽǵĶ�����
��4�����ε�����ѧ���μӻ�����ƽ��ʱ���Ƿ����Ҫ����ʱ�����������λ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y��ax2��2ax��3a��a��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y��������ύ�ڵ�C������ΪD��
��1����D�����꣨�ú�a�Ĵ���ʽ��ʾ����
��2������ADΪֱ����Բ������C��
���������ߵĺ�����ϵʽ��
����ͼ2����E��y�Ḻ������һ�㣬����BE������OBE��ƽ����ijһ����ת180�㣬�õ���PMN����P��M��N�ֱ�͵�O��B��E��Ӧ�������ҵ�M��N�����������ϣ���MF��x���ڵ�F�����߶�MF��BF��1��2�����M��N�����ꣻ
�۵�Q�������ߵĶԳ����ϣ���QΪԲ�ĵ�Բ��A��B���㣬���Һ�ֱ��CD���У���ͼ3�����Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PE=PA��PE��CD��F��
��1����֤�� PC=PE��
��2�����CPE�Ķ�����
��3����ͼ�ڣ���������ABCD��Ϊ����ABCD�������������䣬����ABC=65�㣬���CPE=________�ȣ�
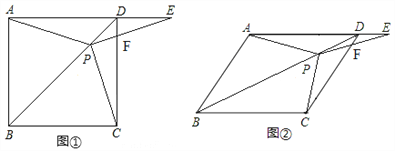
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com