
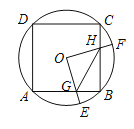
【题目】如图,边长为4的正方形ABCD内接于⊙O,点E是![]() 上的一动点(不与点A、B重合),点F是
上的一动点(不与点A、B重合),点F是![]() 上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
①![]() ;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为
;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为![]() .其中正确的是____________.(把你认为正确结论的序号都填上)
.其中正确的是____________.(把你认为正确结论的序号都填上)
【答案】①②④
【解析】
试题①如图1中,连接OB、OA.
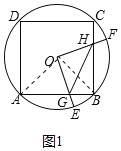
∵四边形ABCD是正方形,
∴∠EOF=∠AOB=90°,
∴∠AOE+∠BOE=∠BOF+∠BOE,
∴∠AOE=∠BOF,
∴![]() .
.
所以①正确;
②如图1中,在△AOG和△BOH中,
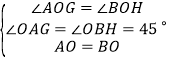 ,
,
∴△AOG≌△BOH;
∴OG=OH,
∵∠GOH=90°,
∴△OGH是等腰直角三角形.
所以②正确;
③如图1中,
∵△AOG≌△BOH,
∴四边形OGBH的面积=△AOB的面积=![]() 正方形ABCD的面积,
正方形ABCD的面积,
∴四边形OGBH的面积不发生变化.
所以③错误;
④∵△AOG≌△BOH,
∴AG=BH,
∴BG+BH=BG+AG=BC=4,
设BG=x,则BH=4-x,
则GH=![]() =
=![]() =
=![]() ,
,
∴当x=2时GH最小,最小值为![]() ,
,
∴△GBH周长的最小值为4+![]() .
.
所以④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m.鸡场的面积能达到150m2吗?如果能,请你给出设计方案;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点,![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
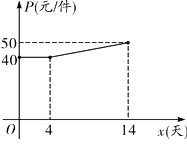
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C在x,y轴正半轴上,反比例函数![]() 过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n).
过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n).
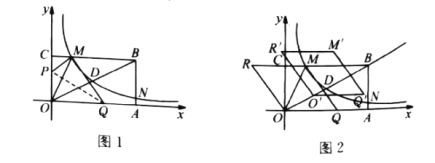
(1)求反比例函数的解析式;
(2)若将矩形一角折叠,使点O与点M重合,折痕为PQ,求点P的坐标;
(3)如图2,若将![]() 沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒
沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒![]() 个单位向上平移t秒.
个单位向上平移t秒.
① 用t的代数式表示![]() 和
和![]() 的坐标;
的坐标;
② 要使该菱形始终与反比例函数图像有交点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
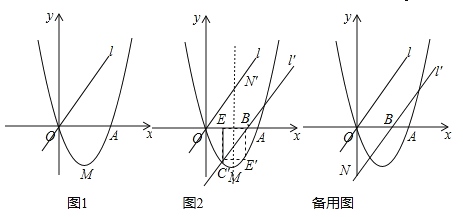
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com