
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 分类讨论:①以OP为底时,点P的个数;②以AP为底时,点P的个数;③以AO为底边时,点P的个数.
解答 解:因为△AOP为等腰三角形,所以可分成三类讨论: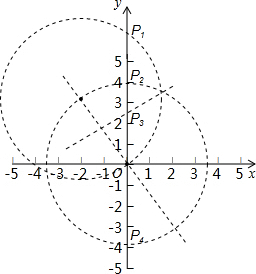
①AO=AP(有一个)
此时只要以A为圆心AO长为半径画圆,可知圆与y轴交于O点和另一个点,另一个点就是P;
②AO=OP(有两个)
此时只要以O为圆心AO长为半径画圆,可知圆与y轴交于两个点,这两个点就是P的两种选择(AO=OP=R)
③AP=OP(一个)
作AO的中垂线,与y轴有一个交点,该交点就是点P的最后一种选择.(利用中垂线性质)
综上所述,共有4个.
故选B
点评 本题考查了等腰三角形的判定、坐标与图形性质;解答该题时,利用了“分类讨论”的数学思想,以防漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
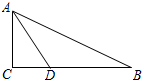 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com