
分析 (1)根据同底数幂的乘除法法则计算即可求解;
(2)先算乘方、负整数指数幂和零指数幂,再算加减法即可求解;
(3)根据同底数幂的乘法法则计算即可求解;
(4)先算幂的乘方和积的乘方、再算同底数幂的乘法,再合并同类项即可求解.
解答 解:(1)-t3•(-t)4÷(-t)5
=t3+4-5
=t2;
(2)(-1)2015+2-1-($\frac{3}{2}$)-2+(π-3.14)0
=-1+$\frac{1}{2}$-$\frac{4}{9}$+1
=$\frac{1}{18}$;
(3)(a-b)2•(a-b)n•(b-a)3
=-(a-b)2+n+3
=-(a-b)5+n;
(4 ) 2(x3)2•x3-(4x3)3+(-3x)4•x5.
=2x6•x3-64x9+81x4•x5
=2x9-64x9+81x9
=19x9.
点评 本题主要考查整式的混合运算,同底数幂的乘法,积的乘方,合并同类项,负整数指数幂、绝对值、零指数幂和乘方的运用,熟记公式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
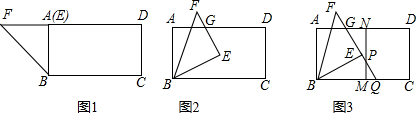
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com