
分析 (1)分式两边都乘以x2-1,然后求出方程的解,最后进行检验;
(2)先提取公因式(2x+1),进而得到(2x+1)(2x+1+3)=0,解一元一次方程求出方程的解.
解答 解:(1)∵$\frac{x+1}{x-1}$-$\frac{6}{{x}^{2}-1}$=1,
∴$\frac{{(x+1)}^{2}}{{{x}^{2}-1}^{\;}}-\frac{6}{{x}^{2}-1}=1$,
∴$\frac{{x}^{2}+2x+1-6}{{x}^{2}-1}=\frac{{x}^{2}-1}{{x}^{2}-1}$,
∴$\frac{{x}^{2}+2x-5}{{x}^{2}-1}-\frac{{x}^{2}-1}{{x}^{2}-1}=0$,
∴$\frac{2x-4}{{x}^{2}-1}=0$,
∴2x-4=0且x2-1≠0,
∴x=2,
经检验x=2是原方程的解;
(2)∵(2x+1)2=-6x-3,
∴(2x+1)2+3(2x+1)=0,
∴(2x+1)(2x+1+3)=0,
∴2x+1=0,2x+4=0,
∴x1=-$\frac{1}{2}$,x2=-2.
点评 本题主要考查了因式分解法解一元二次方程以及解分式方程的知识,解答本题的关键是熟练掌握因式分解解方程的步骤以及注意分式方程要验根,此题难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
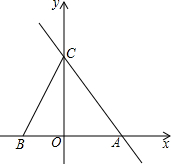 直线y=-2x+b与x轴、y轴分别交与点A、C,点B(-2,0),AB=$\frac{5}{6}$CO.
直线y=-2x+b与x轴、y轴分别交与点A、C,点B(-2,0),AB=$\frac{5}{6}$CO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com