Question

5．直线y=-2x+b与x轴、y轴分别交与点A、C，点B（-2，0），AB=$\frac{5}{6}$CO．
（1）求A点坐标；
（2）动点P从A点出发以$\sqrt{5}$个单位/s的速度沿线段AC向终点C运动，过P作PH⊥AC交y轴正半轴于H，设线段PH长为y，运动时间为t，求y与t的函数关系式，（并写出自变量的取值范围）；
（3）在（2）的条件下，作射线BK平分∠CBP，交线段AC于点K，过点C作BK的垂线交射线BP于点Q，当t为何值时，AC•PQ=QK•BC，并直接写出以P为心，线段PH为半径的圆与x轴的位置关系．

Answer 1

分析 （1）根据y=-2x+b与x轴、y轴交点坐标，可得点A的坐标为（$\frac{b}{2}$，0），点C的坐标为（0，b），再由AB=$\frac{5}{6}$CO得出b的值，代入即可；
（2）根据勾股定理，可得AC的长，再根据相似三角形的判定与性质，可得函数解析式，根据0＜AP＜AC，可得自变量的取值范围；
（3）由角平分线垂直于三角形的边，得到三角形是等腰三角形，根据等腰三角形的性质得到BC=BQ，∠QCB=∠BQC，同理可证∠QCK=∠CQK，因为AC•PQ=QK•BC，
得到∠BCA=∠BQK，得到△ABC∽△KQP，根据相似三角形的性质证得∠BAC=∠PQK，∠KQP=∠ACB，所以QK∥AB，∠KQP=∠PBA，∠KQP=∠ACB，因为∠BAC=∠BAC
，得到△ABC∽△APB，根据比例式列出方程，求得t的值，因为点P在AC上，直线AC的解析式：y=-2x+6，得到P点的纵坐标，即为点P到x轴的距离，比较与PH的大小，得出以P为心，线段PH为半径的圆与x轴的位置关系．

解答 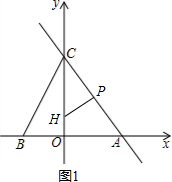解：（1）令y=0，则x=$\frac{b}{2}$，令x=0．则y=b，
∴点A的坐标为（$\frac{b}{2}$，0）点C的坐标为（0，b），
∵AB=2+|$\frac{b}{2}$|，$\frac{5}{6}$CO=$\frac{5}{6}$×|b|，
∴2+|$\frac{b}{2}$|=$\frac{5}{6}$×|b|，
解得：b=6，
所以点A的坐标为（3，0）；

（2）如图1，
∵点A的坐标为（3，0）点C的坐标为（0，6），
∴OA=3，OC=6，
∴AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=3$\sqrt{5}$，
∴PC=3$\sqrt{5}$-$\sqrt{5}$t，
∵PH⊥AC，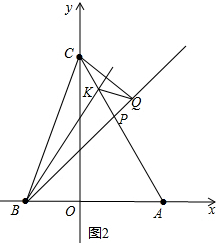
∴∠CPH=∠COA=90°，∠PCH=∠OCA，
∴△PCH∽△OCA，
∴$\frac{PH}{OA}$=$\frac{CP}{OC}$，即$\frac{y}{3}$=$\frac{3\sqrt{5}-\sqrt{5}t}{6}$
∴y=$-\frac{{\sqrt{5}}}{2}t+\frac{{3\sqrt{5}}}{2}$ （$\frac{3}{5}$＜t＜3）．

（3）如图2∵BK平分∠CBP，BK⊥CQ，
∴BC=BQ，
∴∠QCB=∠BQC，同理可证∠QCK=∠CQK，
∴∠BCA=∠BQK，
∵AC•PQ=QK•BC，
∴$\frac{AC}{QK}$=$\frac{BC}{PQ}$，
∴△ABC∽△KQP，
∴∠BAC=∠PQK，∠KQP=∠ACB，
∴QK∥AB，
∴∠KQP=∠PBA，
∴∠KQP=∠ACB，∵∠BAC=∠BAC，
∴△ABC∽△APB，
∴$\frac{AP}{AB}$=$\frac{AB}{AC}$，
∵AP=$\sqrt{5}$t，AB=5，AC=3$\sqrt{5}$，
∴$\frac{\sqrt{5}t}{5}$=$\frac{5}{3\sqrt{5}}$，∴t=$\frac{5}{3}$，
∴PH=y=$-\frac{{\sqrt{5}}}{2}t+\frac{{3\sqrt{5}}}{2}$=$\frac{4\sqrt{5}}{6}$，
∵点P在AC上，直线AC的解析式：y=-2x+6，
设P的坐标（a，-2a+6），
由勾股定理得；（3-a）²+（-2a+6）²=${（\frac{5\sqrt{5}}{3}）}^{2}$，
解得a=$\frac{14}{3}$，a=-$\frac{4}{3}$（舍去），
∴-2a+6＞$\frac{4\sqrt{5}}{6}$，
∴以P为心，线段PH为半径的圆与x轴的位置关系是相离．

点评 本题主要考查了平面直角坐标系中求点的坐标，解方程，三角形相似的判定和性质，等腰三角形的性质，用待定系数法求一次函数的解析式以及圆与直线的位置等知识点．