
分析 先由勾股定理求出b,再根据三角函数的定义即可求解.
解答 解:∵在Rt△ABC中,∠C=90°,a=2,c=6,
∴b=$\sqrt{{c}^{2}-{a}^{2}}$=4$\sqrt{2}$,
∴sinA=$\frac{a}{c}$=$\frac{2}{6}$=$\frac{1}{3}$,
cosA=$\frac{b}{c}$=$\frac{4\sqrt{2}}{6}$=$\frac{2\sqrt{2}}{3}$,
tanA=$\frac{a}{b}$=$\frac{2}{4\sqrt{2}}$=$\frac{\sqrt{2}}{4}$.
点评 本题考查了锐角三角函数的定义:在Rt△ABC中,∠C=90°,
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.即sinA=∠A的对边:斜边=a:c;
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.即cosA=∠A的邻边:斜边=b:c;
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.即tanA=∠A的对边:∠A的邻边=a:b.
也考查了勾股定理.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
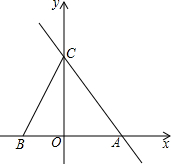 直线y=-2x+b与x轴、y轴分别交与点A、C,点B(-2,0),AB=$\frac{5}{6}$CO.
直线y=-2x+b与x轴、y轴分别交与点A、C,点B(-2,0),AB=$\frac{5}{6}$CO.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com