
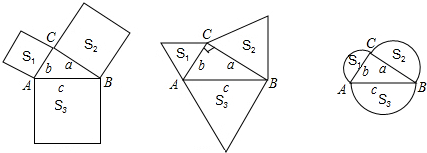
分析 分别根据正方形的面积公式,等边三角形的面积公式及半圆的面积公式,先用含有a,b,c的式子,表示S1,S2,S3,然后根据S1+S2=S3,得到a,b,c的关系,最后根据勾股定理的逆定理,即可判断△ABC是直角三角形.
解答 解:(1)∵S1+S2=S3,S1=AC2,S2=BC2,S3=AB2,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)∵S1+S2=S3,S1=$\frac{\sqrt{3}}{4}$AC2,S2=$\frac{\sqrt{3}}{4}$BC2,S3=$\frac{\sqrt{3}}{4}$AB2,
∴$\frac{\sqrt{3}}{4}$AC2+$\frac{\sqrt{3}}{4}$BC2=$\frac{\sqrt{3}}{4}$AB2,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(3)∵S1+S2=S3,S1=$\frac{π}{8}$AC2,S2=$\frac{π}{8}$BC2,S3=$\frac{π}{8}$AB2,
∴$\frac{π}{8}$AC2+$\frac{π}{8}$BC2=$\frac{π}{8}$AB2,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
点评 本题考查了勾股定理的逆定理及正方形面积公式,等边三角形的面积公式,及圆的面积公式的运用,解题关键是明确此题中①图中三角形的边长的平方即为相应的正方形的面积,②图中三角形的边长的平方的$\frac{\sqrt{3}}{4}$倍,即为相应的等边三角形的面积,③图中三角形的边长的平方的$\frac{π}{8}$倍,即为相应的半圆的面积.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
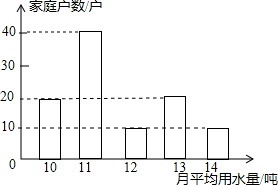 某市自来水公司对某小区500户家庭的用水情况作一次调查,随机抽查了小区100户家庭一年的越平均用水量(单位:吨),并将调查结果绘制成如图所示的条形图)
某市自来水公司对某小区500户家庭的用水情况作一次调查,随机抽查了小区100户家庭一年的越平均用水量(单位:吨),并将调查结果绘制成如图所示的条形图)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
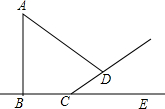 九(1)班的同学到郊外展开活动,在土坡旁看见一棵古树,班上同学很想知道古树AB的高.小王拿尺子量得古树在地面上的影子BC=8米,在斜坡上面的影子CD=6米,测得斜坡CD与地面成∠DCE=30°,同一时刻小李量的1.5米的旗杆在地上面的影子长是2米.请你根据以上数据算出古树的高.
九(1)班的同学到郊外展开活动,在土坡旁看见一棵古树,班上同学很想知道古树AB的高.小王拿尺子量得古树在地面上的影子BC=8米,在斜坡上面的影子CD=6米,测得斜坡CD与地面成∠DCE=30°,同一时刻小李量的1.5米的旗杆在地上面的影子长是2米.请你根据以上数据算出古树的高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
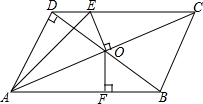 如图,在?ABCD中,BD是对角线,且BD⊥AD,OA=10cm,DB=12cm,OE⊥AC交CD于E,OF⊥AB于F
如图,在?ABCD中,BD是对角线,且BD⊥AD,OA=10cm,DB=12cm,OE⊥AC交CD于E,OF⊥AB于F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com