
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在y轴上,点O,B1,B2,B3…都在直线l上,则点B2017的坐标是(2017$\sqrt{3}$,2017).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在y轴上,点O,B1,B2,B3…都在直线l上,则点B2017的坐标是(2017$\sqrt{3}$,2017). 分析 根据题意得出B1的坐标,进而得出B2,B3坐标,进而得出坐标变化规律,进而得出答案.
解答 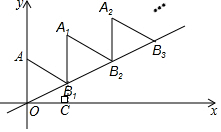 解:过点B1 作B1 C⊥x轴,
解:过点B1 作B1 C⊥x轴,
∵△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,
∴OB1=2,∠AOB1=60°,∠B1 OC=30°,
∴OC=OB1 cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,CB1=OB1 sin30°=2×$\frac{1}{2}$=1,
∴B1的坐标为($\sqrt{3}$,1),
∴B2的坐标为(2$\sqrt{3}$,2),B3的坐标为(3$\sqrt{3}$,3),B4的坐标为(4$\sqrt{3}$,4),
…
∴B2017的坐标是(2017$\sqrt{3}$,2017).
故答案为(2017$\sqrt{3}$,2017).
点评 此题主要考查了一次函数图象上点的坐标特征以及数字变化类,得出坐标变化规律是解题关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题
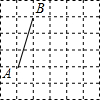 如图,在所给的6×6网格中每个小正方形的边长都为1,线段AB的端点都在格点上,按下列要求画正方形(另两个顶点也都在格点上),并直接写出所画正方形的面积.
如图,在所给的6×6网格中每个小正方形的边长都为1,线段AB的端点都在格点上,按下列要求画正方形(另两个顶点也都在格点上),并直接写出所画正方形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|m|=|n|,则m=n | B. | 若a2>b2,则a>b | C. | 若$\root{3}{a}=\root{3}{b}$,则a=b | D. | 若$\sqrt{a^2}={(\sqrt{b})^2}$,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
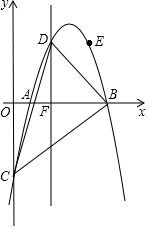 如图,抛物线y=-x2+ax+b经过点A(1,0),B(5,0),与y轴交于点C,直线DF与x轴垂直,与抛物线交于点D,其横坐标为2,点E与点D关于抛物线的对称轴对称.
如图,抛物线y=-x2+ax+b经过点A(1,0),B(5,0),与y轴交于点C,直线DF与x轴垂直,与抛物线交于点D,其横坐标为2,点E与点D关于抛物线的对称轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
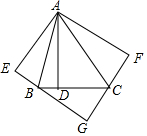 如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.
如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1>b-1 | B. | -a>-b | C. | |a|>|b| | D. | -$\frac{a}{2}$>-$\frac{b}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com