
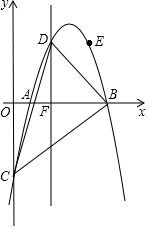
 如图,抛物线y=-x2+ax+b经过点A(1,0),B(5,0),与y轴交于点C,直线DF与x轴垂直,与抛物线交于点D,其横坐标为2,点E与点D关于抛物线的对称轴对称.
如图,抛物线y=-x2+ax+b经过点A(1,0),B(5,0),与y轴交于点C,直线DF与x轴垂直,与抛物线交于点D,其横坐标为2,点E与点D关于抛物线的对称轴对称.分析 (1)根据待定系数法,可得函数解析式,根据自变量与函数值得对应关系,可得D点坐标,根据点关于对称轴对称,可得答案;
(2)根据待定系数法,可得CD的解析式,根据自变量与函数值的对应关系,可得F点坐标,根据三角形的面积,可得答案;
(3)分别以点C、M、N为直角顶点分三类进行讨论,利用全等三角形和勾股定理ON的长即可.
解答 解:(1)将A,B点的坐标代入函数解析式$\left\{\begin{array}{l}{-1+a+b=0}\\{-25+5a+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=6}\\{b=-5}\end{array}\right.$,
抛物线的解析式为y=-x2+6x-5,
y=-(x-3)2+4,对称轴是x=3,
当x=2时,y=-22+2×6-5=3,即D点的坐标是(2,3),
点E与点D关于抛物线的对称轴对称,得
E点坐标(4,3);
(2)如图1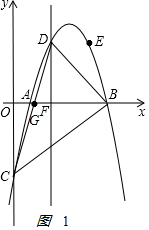 ,
,
CD的解析式为y=4x-5,
当y=0时,x=$\frac{5}{4}$,即F($\frac{5}{4}$,0),
BF=5-$\frac{5}{4}$=$\frac{15}{4}$,
S△DBC=$\frac{1}{2}$BF(yD-yC)
=$\frac{1}{2}$×$\frac{15}{4}$×(3+5)=15;
(3)以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
①以点M为直角顶点且M在x轴上方时,如图2,EM=MN,∠CMN=90°,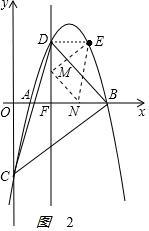
则△EDM≌△MFN,
∴DE=MF=2,FN=DM=DE-MF=3-2=1,
NO=OF+FN=2+1=3
∴N(3,0);
②以点M为直角顶点且M在x轴下方时,如图3,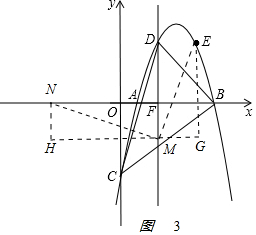
作辅助线,构建如图所示的两直角三角形:Rt△NHM和Rt△MGE,
得Rt△NHM≌Rt△MGE,
∴HM=EG=5,
∵OH=1,
∴ON=NF-OF=5-2=3,
∴N(-3,0);
③以点N为直角顶点且N在y轴左侧时,如图4,CN=MN,∠MNC=90°,作辅助线,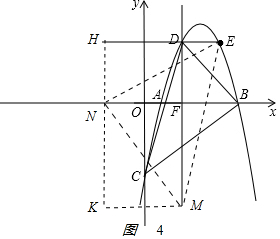
同理得Rt△NKM≌Rt△EHN,
∴MK=NF=HN=3,
∴ON=FN-OF=3-2=1,
∴N(-1,0);
④以点N为直角顶点且N在y轴右侧时,作辅助线,如图5,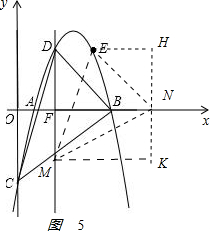
同理得MK=HN=NF=3,
∴ON=OF+FN=2+3=5,
∴N(5,0);
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;
综上可知当△CMN为等腰直角三角形时N点坐标为(3,0)或(-3,0)或(-1,0)或(5,0).
点评 本题为二次函数的综合应用,主要涉及待定系数法、三角形的面积、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理、方程思想及分类讨论思想等知识点.在(1)中注意待定系数法的应用,在(2)中求出FB的长是解题关键;在(3)中分三种情况分别求得ON的长是解题的关键.本题考查知识点较多,综合性较强,难度较大.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
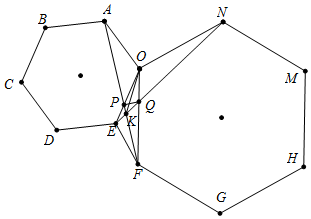 如图所示:以△OEF的两边OE,OF为边向外作两个正六边形,正六边形OABCDE,正六边形OFGHMN.则下列结论正确的是:①△EON≌△AOF;②∠AKE=90°;③△PKQ为等边三角形;④PQ∥EF;⑤OK平分∠EOF,则下列选项正确的是( )
如图所示:以△OEF的两边OE,OF为边向外作两个正六边形,正六边形OABCDE,正六边形OFGHMN.则下列结论正确的是:①△EON≌△AOF;②∠AKE=90°;③△PKQ为等边三角形;④PQ∥EF;⑤OK平分∠EOF,则下列选项正确的是( )| A. | ①、②、③、④、⑤ | B. | ②、③、④ | C. | ①、⑤ | D. | ③、④、⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在y轴上,点O,B1,B2,B3…都在直线l上,则点B2017的坐标是(2017$\sqrt{3}$,2017).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在y轴上,点O,B1,B2,B3…都在直线l上,则点B2017的坐标是(2017$\sqrt{3}$,2017).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
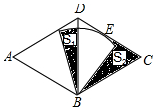 如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2-S1=2$\sqrt{3}$-π.
如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2-S1=2$\sqrt{3}$-π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\frac{x}{a}$<$\frac{y}{a}$,则x<y | B. | 若bx>by,则x>y | C. | 若$\frac{x}{a}$=$\frac{y}{a}$,则x=y | D. | 若mx=my,则x=y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com