
 如图,一拱桥呈抛物线状,桥的最大高度是16m,跨度是40m,求在线段AB上离中心M处15m的地方,桥的高度是多少?
如图,一拱桥呈抛物线状,桥的最大高度是16m,跨度是40m,求在线段AB上离中心M处15m的地方,桥的高度是多少? 分析 以AB为x轴,点M为坐标原点作出平面直角坐标系,表示出A点坐标,C点坐标,设出抛物线的解析式,代入点求出解析式,再进一步代入数值解答即可.
解答 解:如图,建立平面直角坐标系,
点A的坐标是(-20,0),点C的坐标是(0,16),
设抛物线的解析式为y=ax2+k,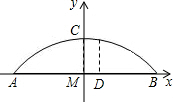
把点A、C代入函数解析式得
$\left\{\begin{array}{l}{400a+k=0}\\{k=16}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{25}}\\{k=16}\end{array}\right.$.
因此抛物线的解析式为y=-$\frac{1}{25}$x2+16,
把D(15,0)点的横坐标代入y=-$\frac{1}{25}$x2+16=7(米),
答:桥的高度是7m.
点评 此题考查利用抛物线的特点建立平面直角坐标系,求出抛物线解析式,进一步利用解析式解决问题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C是∠ABC一边上一点
如图,点C是∠ABC一边上一点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com