
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②![]() ;③
;③![]() =PHPB;④tan∠DBE=
=PHPB;④tan∠DBE=![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
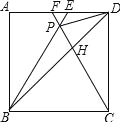
【答案】①③④.
【解析】
试题分析:由正方形的性质和相似三角形的判定与性质,即可得出结论.∵△BPC是等边三角形,∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD中,∵AB=BC=CD,∠A=∠ADC=∠BCD=90°,∴∠ABE=∠DCF=30°,∴∠CPD=∠CDP=75°,∴∠PDE=15°,∵∠PBD=∠PBC﹣∠HBC=60°﹣45°=15°,∴∠EBD=∠EDP,∵∠DEP=∠DEB,∴△BDE∽△DPE;故①正确;∵PC=CD,∠PCD=30°,∴∠PDC=75°,∴∠FDP=15°,∵∠DBA=45°,∴∠PBD=15°,∴∠FDP=∠PBD,∵∠DFP=∠BPC=60°,∴△DFP∽△BPH,∴![]() ,故②错误;∵∠PDH=∠PCD=30°,∵∠DPH=∠DPC,∴△DPH∽△CDP,∴
,故②错误;∵∠PDH=∠PCD=30°,∵∠DPH=∠DPC,∴△DPH∽△CDP,∴![]() ,∴
,∴![]() =PHCD,∵PB=CD,∴
=PHCD,∵PB=CD,∴![]() =PHPB,故③正确;如图,过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,∴∠PCD=30°,∴CM=PN=PBsin60°=4×
=PHPB,故③正确;如图,过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,∴∠PCD=30°,∴CM=PN=PBsin60°=4×![]() =
=![]() ,PM=PCsin30°=2,∵DE∥PM,∴∠EDP=∠DPM,∴∠DBE=∠DPM,∴tan∠DBE=tan∠DPM=
,PM=PCsin30°=2,∵DE∥PM,∴∠EDP=∠DPM,∴∠DBE=∠DPM,∴tan∠DBE=tan∠DPM=![]() =
=![]() ,故④正确.
,故④正确.
故答案为:①③④.


科目:初中数学 来源: 题型:
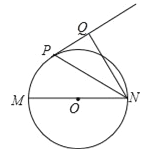
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP=![]() ,求NQ的长.
,求NQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润为120元,为了扩大销量,尽快减少库存,超市准备适当降价,据测算,若每箱降价2元,则每天可多售出4箱.
(1)如果要使每天销售该饮料获利14000元,则每箱应降价多少元.
(2)每天销售该饮料获利能达到14500元吗?若能,则每箱应降价多少?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
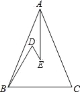
【题目】如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( ).
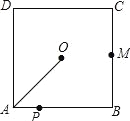
A.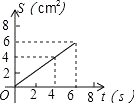 B.
B.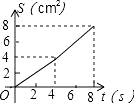
C.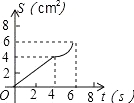 D.
D.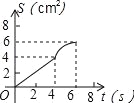
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为__.
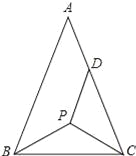
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() 与抛物线y=
与抛物线y=![]() +bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
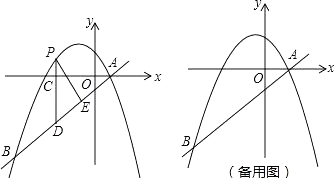
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算结果正确的是( )
A. 2a+3b=5ab B. ﹣2xy﹣3xy= ﹣xy
C. 6x3+4x7=10x10 D. 8a2b﹣8ba2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.
(1)若k=4,PA=15,则四边形PARA′的形状是 ;
(2)设DR=x,点B关于直线PQ的对称点为B′点.
①记△PRA′的面积为S1,△PQB′的面积为S2.当S1<S2时,求相应x的取值范围及S2﹣S1的最大值;(用含k的代数式表示)
②在点P的运动过程中,判断点B′能否与点A′重合?请说明理由.
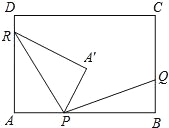
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com