
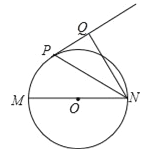
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP=![]() ,求NQ的长.
,求NQ的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连结OP,根据切线的性质由直线PQ与⊙O相切得OP⊥PQ,再由OP=ON得到∠ONP=∠OPN,由NP平分∠MNQ得到∠ONP=∠QNP,利用等量代换得∠OPN=∠QNP,根据平行线的判定得OP∥NQ,所以NQ⊥PQ;
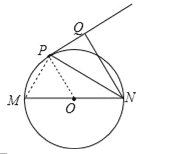
(2)连结PM,根据圆周角定理由MN是⊙O的直径得到∠MPN=90°,易证得Rt△NMP∽Rt△NPQ,然后利用相似比可计算出NQ的长.
试题解析:(1)证明:连结OP,如图,∴直线PQ与⊙O相切,∴OP⊥PQ,∵OP=ON,∴∠ONP=∠OPN,∵NP平分∠MNQ,∴∠ONP=∠QNP,∴∠OPN=∠QNP,∴OP∥NQ,∴NQ⊥PQ;
(2)连结PM,如图,∵MN是⊙O的直径,∴∠MPN=90°,∵NQ⊥PQ,∴∠PQN=90°,而∠MNP=∠QNP,∴Rt△NMP∽Rt△NPQ,∴![]() ,即
,即![]() ,∴NQ=3.
,∴NQ=3.


科目:初中数学 来源: 题型:
【题目】下列说法中,(1)﹣a 一定是负数;(2)|﹣a|一定是正数;(3)倒数等于它本身的数是±1;(4)绝对值等于它本身的数是 1.其中正确的个数是( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民用水情况,在某小区随机抽查了15户家庭的月用水量,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 9 |
户数 | 2 | 5 | 6 | 1 | 1 |
则这15户家庭的月用水量的众数与中位数分别为( )
A.5、5B.5、6C.6、6D.9、6
查看答案和解析>>
科目:初中数学 来源: 题型:
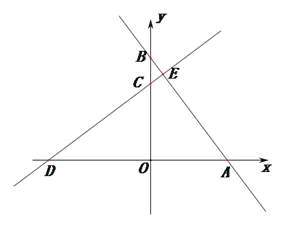
【题目】(本题满分12分) 在平面直角坐标系中,直线![]() 交
交![]() 轴、
轴、![]() 轴分别于点
轴分别于点![]() 、点
、点![]() ,将△
,将△![]() 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转![]() 得到△
得到△![]() .直线
.直线![]() 交直线
交直线![]() 于点
于点![]() ,如图1.
,如图1.
(1))求:直线![]() 的函数关系式.
的函数关系式.
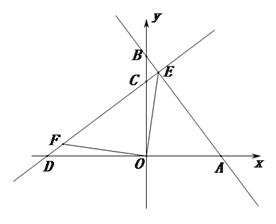
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,如图2.
,如图2.
① 求证: ![]() =
=![]() .
.
② 求:点![]() 的坐标.
的坐标.
(3)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是
是![]() 轴上一点(点
轴上一点(点![]() 不与点
不与点![]() 重合),当△
重合),当△![]() 和△
和△![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
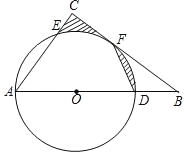
【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
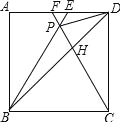
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②![]() ;③
;③![]() =PHPB;④tan∠DBE=
=PHPB;④tan∠DBE=![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com