
【题目】(本题满分12分) 在平面直角坐标系中,直线![]() 交
交![]() 轴、
轴、![]() 轴分别于点
轴分别于点![]() 、点
、点![]() ,将△
,将△![]() 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转![]() 得到△
得到△![]() .直线
.直线![]() 交直线
交直线![]() 于点
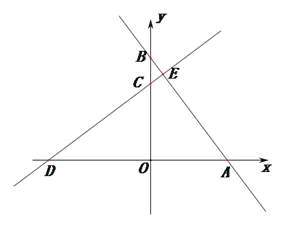
于点![]() ,如图1.
,如图1.
(1))求:直线![]() 的函数关系式.
的函数关系式.
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
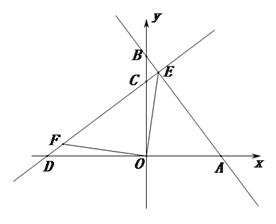
于点![]() ,如图2.
,如图2.
① 求证: ![]() =
=![]() .
.
② 求:点![]() 的坐标.
的坐标.
(3)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是
是![]() 轴上一点(点
轴上一点(点![]() 不与点
不与点![]() 重合),当△
重合),当△![]() 和△
和△![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.
![]()
![]()
【答案】(1)![]() (2)①见解析;②
(2)①见解析;②![]() ;(3)
;(3)![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(1)先求出A,B点坐标,根据旋转90°,再求出C,D点坐标,待定系数法求一元一次函数.
(2) ①先证△DFO≌△BOE,可得OF=OE , 再利用等边对等角,求得∠OEF=45°.
② 先联立方程组,求点E(![]() 再构造全等,求出点F (
再构造全等,求出点F (![]() ).
).
(3)利用全等和中点坐标公式,可求得P点坐标,P点有多解情况,要分类讨论.
试题解析:
![]() ,
,
令x=0,B(0,4),令y=0,A(3,0),则D(-4,0),C(0, ![]()
解设过D,C直线解析式是![]() ,
,
![]() ,
,
解得 ,
,
![]() .
.
(2)①![]() ,
,
![]()
![]() ,
,
△![]() 旋转了90°,所以
旋转了90°,所以![]() ,
, ![]() ,
,
 ,
,
![]() △DFO≌△BOE,可得OF=OE ,
△DFO≌△BOE,可得OF=OE ,
![]() ∠OEF=45°.
∠OEF=45°.
②联立,解得E(
![]() ,由①知,△DFO≌△BOE,
,由①知,△DFO≌△BOE,
所以旋转以后得F (![]() ).
).
P(-8,-3 ),( ![]() ,(
,( ![]()

如图,与![]() CDO面积相等(也就是全等)满足题意的三角形有三个,
CDO面积相等(也就是全等)满足题意的三角形有三个,
在![]() ,,D(-4,0)点是C(0,3)和
,,D(-4,0)点是C(0,3)和![]() 中点,
中点, ![]() ,
,![]() ,
,
所以有![]() ,
,
在![]() ,由题意知
,由题意知![]() ,(1,0),OD=O
,(1,0),OD=O![]() ,勾股定理知,P3纵坐标
,勾股定理知,P3纵坐标![]() ,代入直线
,代入直线![]() ,得到P3(
,得到P3(![]() ))
))
在![]() 由题意知D(-4,0)是
由题意知D(-4,0)是![]() (x,y),P3(
(x,y),P3(![]() )中点,
)中点, ![]() =-4,
=-4, ![]() =0,
=0,  ,
,
所以![]() ,
,
所以P的坐标是, ![]() ,
, ![]() ,
, ![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题: 

(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
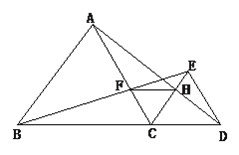
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2). 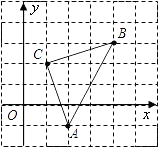
(1)写出点A,B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
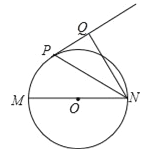
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP=![]() ,求NQ的长.
,求NQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店出售一种优惠卡,花200元买这种卡后,凭卡可以在这家商店按8折购物,下列情况买购物卡合算的是( )
A. 购物高于800元 B. 购物低于800元 C. 购物高于1 000元 D. 购物低于1 000元
查看答案和解析>>
科目:初中数学 来源: 题型:
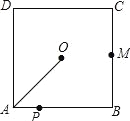
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( ).
A.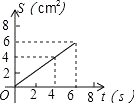 B.
B.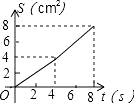
C.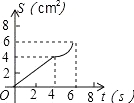 D.
D.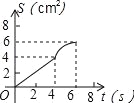
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com