
����Ŀ��ij��ѧΪ�˽�ȫУѧ����У��ѧ�ķ�ʽ����ȫУ�����ȡ��������ѧ�������ʾ����飮�ʾ�������������ѧ��ʽ��ѧ��ѡ��ÿ��ֻ��ѡһ��Ҳ��ܲ�ѡ��ͬʱ�ѵ���õ��Ľ�����Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ�������������������ͼ���ṩ����Ϣ����������⣺ 

��1������ε����У�һ����ȡ�˶�����ѧ����
��2��ͨ�����㲹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�������������������Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��4����ȫУ��1600��ѧ�������Ƹ�У����˽�ҳ���ѧ��ѧ��Լ�ж�������
���𰸡�
��1��80
���24��30%=80���������ʴ�Ϊ��80����
��2�����80��20%=16��������
��ȫ����ͳ��ͼ����ͼ��ʾ��
��3��117��
��𣺣�3����������ã�360��� =117�㣬
��������ͳ��ͼ�У�������������������Ӧ��Բ�Ľ�Ϊ117�㣻
��4��200
��𣺸�������ã�1600�� =200��������
���Թ��Ƹ�У����˽�ҳ���ѧ��ѧ��Լ��200����
����������1��������ѧ��ʽΪ���г�������������ռ�İٷֱȣ��õ������ѧ��������2���������������Բ��еİٷֱ�������е���������ȫ����ͳ��ͼ����3�����������������ռ�İٷֱȣ�����360�ȵõ�Բ�ĽǵĶ�������4�������˽�ҳ�����ѧ�İٷֱȣ�����������1600�õ��𰸣�


 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
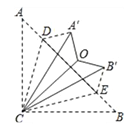
����Ŀ����ͼ������ABC�У�AC=BC����ACB=90������D��E��AB�ϣ�����ACD����BCE�ֱ���CD��CE���ۣ���A��B�ֱ����ڵ�A����B����λ�ã��ٽ���A��CD����B��CE�ֱ���A��C��B��C���ۣ���D���Eǡ���غ��ڵ�O�����A��OB���Ķ�����_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
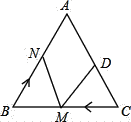
����Ŀ����ͼ���ڵȱ���ABC�У�AB=AC=BC=10���ף�DC=4���ף������M��3����/����ٶ��˶���
��1�������M���߶�CB���ɵ�C���B�˶�����N���߶�BA����B����A���˶�������ͬʱ����������N���˶��ٶ����M���˶��ٶ���ȣ�
�پ���2�����BMN����CDM�Ƿ�ȫ�ȣ���˵�����ɣ�
�ڵ�������˶�ʱ��Ϊ����ʱ����BMN��һ��ֱ�������Σ�
��2������N���˶��ٶ����M���˶��ٶȲ���ȣ���N�ӵ�B��������M��ԭ�����˶��ٶȴӵ�Cͬʱ��������˳ʱ������ABC�����˶�������25���M���N��һ�����������N���˶��ٶ����� ������/�룮��ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
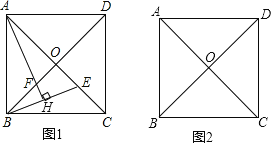
����Ŀ����ͼ����֪������ABCD��AC��BD�ཻ�ڵ�O��EΪAC��һ�㣬AH��EB��EB�ڵ�H��AH��BD�ڵ�F��
��1������E��ͼ1��λ�ã��ж�OE��OF��������ϵ����֤����Ľ��ۣ�
��2������E��AC���ӳ����ϣ�����ͼ2�а���ĿҪ��ȫͼ�Σ��ж�OE��OF��������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹������ϡ�ƻ�����㽶����ˮ��һ���µ���������ijˮ�����������ˮ��7���������������ͳ�ƣ�ͳ�ƽ����ͼ��ʾ�� 
��1�������ϡ�ƻ�����㽶���ۼ۷ֱ���6Ԫ/ǧ�ˡ�8Ԫ/ǧ�˺�3Ԫ/ǧ�ˣ�����7�����۶�����ˮ��Ʒ������
��2������һ���£���30����㣩��ˮ���������ƻ������ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
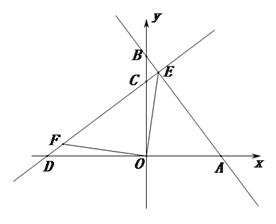
����Ŀ������������12�֣� ��ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ������
������![]() ������ԭ����ʱ����ת
������ԭ����ʱ����ת![]() �õ���
�õ���![]() .ֱ��
.ֱ��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ,��ͼ1.
,��ͼ1.
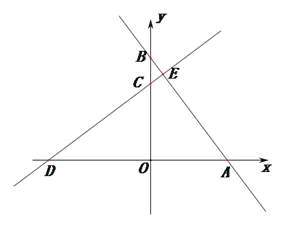
��1������ֱ��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����ͼ2������![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����ͼ2.
����ͼ2.
�� ��֤�� ![]() =
=![]() ��
��
�� ��![]() �����꣮
�����꣮
��3������![]() ��ֱ��
��ֱ��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ����һ�㣨��
����һ�㣨��![]() �����
�����![]() �غϣ�������
�غϣ�������![]() �͡�
�͡�![]() ȫ��ʱ��ֱ��д����
ȫ��ʱ��ֱ��д����![]() ������.
������.
![]()
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com