
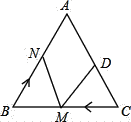
����Ŀ����ͼ���ڵȱ���ABC�У�AB=AC=BC=10���ף�DC=4���ף������M��3����/����ٶ��˶���
��1�������M���߶�CB���ɵ�C���B�˶�����N���߶�BA����B����A���˶�������ͬʱ����������N���˶��ٶ����M���˶��ٶ���ȣ�
�پ���2�����BMN����CDM�Ƿ�ȫ�ȣ���˵�����ɣ�
�ڵ�������˶�ʱ��Ϊ����ʱ����BMN��һ��ֱ�������Σ�
��2������N���˶��ٶ����M���˶��ٶȲ���ȣ���N�ӵ�B��������M��ԭ�����˶��ٶȴӵ�Cͬʱ��������˳ʱ������ABC�����˶�������25���M���N��һ�����������N���˶��ٶ����� ������/�룮��ֱ��д���𰸣�
���𰸡���1������BMN�ա�CDM�����ɼ��������ڵ�t=![]() ���t=
���t=![]() ��ʱ����BMN��ֱ�������Σ���2��3.8��2.6��
��ʱ����BMN��ֱ�������Σ���2��3.8��2.6��
������������������ٸ��������CM=BN=6CM������BM=4CM=CD�����ݡ�SAS��֤����BMN�ա�CDM��
�����˶�ʱ��Ϊt�룬�ֱ��ʾCM��BN��������������������������ε�������⣺I����NMB=90�㣻��BNM=90�㣻
��2����M���N��һ�������������ֿ��ܣ�I����M�˶��ٶȿ죻��N�˶��ٶȿ죮�ֱ��з�����⣮
�����������1���١�BMN�ա�CDM���������£�
��VN=VM=3����/�룬��t=2�룬
��CM=2��3=6��cm����
BN=2��3=6��cm����
BM=BC��CM=10��6=4��cm����
��BN=CM��
��CD=4��cm����
��BM=CD��
����ABC�ǵȱ������Σ�
���B=��C=60�㣬
����BMN����CDM��
BN=CM����B=��C��BM=CD��
���BMN�ա�CDM����SAS��.
�����˶�ʱ��Ϊt�룬��BMN��ֱ�������������������
����NMB=90��ʱ��
�ߡ�B=60�㣬
���BNM=90�㩁��B=90�㩁60��=30�㣮
��BN=2BM��
��3t=2����10��3t����
��t=![]() ���룩��
���룩��
����BNM=90��ʱ��
�ߡ�B=60�㣬
���BMN=90�㩁��B=90�㩁60��=30�㣮
��BM=2BN��
��10��3t=2��3t��
��t=![]() ���룩��
���룩��
�൱t=![]() ���t=
���t=![]() ��ʱ����BMN��ֱ�������Σ�
��ʱ����BMN��ֱ�������Σ�
��2��������������ۣ�
I������M�˶��ٶȿ죬�� 3��25��10=25VN����� VN=2.6��
������N�˶��ٶȿ죬�� 25VN��20=3��25����� VN=3.8��
�ʴ�Ϊ 3.8��2.6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��350��ְ�����������ص��飬��ͼ�ǵ�������ͳ��ͼ�������ͳ��ͼ�ṩ����Ϣ���ش��������⣺ 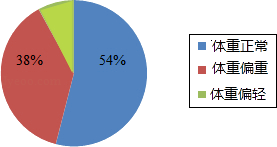
��1������������ְ��ռ�İٷֱ�����
��2����������������ƫ�ص�ְ����ռ%��
��3������ƫ���ְ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����꼶����������������ȤС�飬ÿ���μ���ֻ�ܲμ�һ����ȤС�飬��ͼ��������ȤС�鲻������Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ������ͼ����Ϣ���ɵ����н��۲���ȷ���ǣ� �� 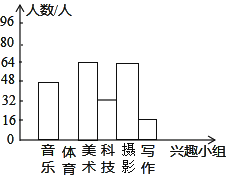

A.���꼶����320�˲μ�����ȤС��
B.������ȤС���Ӧ����Բ�ĽǵĶ���Ϊ96��
C.������ȤС���Ӧ����Բ�ĽǵĶ���Ϊ72��
D.��С��������ɵ�����д�����������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
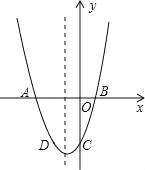
����Ŀ����֪�����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬����A������Ϊ����3��0������y�ύ�ڵ�C����D����2����3�����������ϣ�
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ�������һ����P�����PA+PD����Сֵ��
��3��������������һ����P��ʹ������ABP�����Ϊ6����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�������ȷ���ǣ� ��
A. 0�������������Ǹ��� B. O����С������
C. 0�����ĸ��� D. 0�Ȳ���������Ҳ���Ǹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
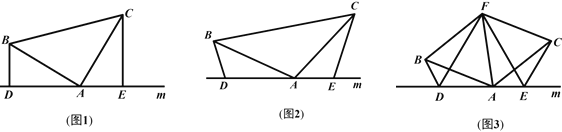
����Ŀ����1����ͼ1����֪������ABC�У���BAC=90�㣬AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E��֤����DE��BD+CE��
��2����ͼ2������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ����ҡ�BDA����AEC����BAC������������Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ�������������������֤����������������˵�����ɣ�
��3����չ��Ӧ�ã���ͼ3��D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E����
�����غϣ�����FΪ��BACƽ�����ϵ�һ�㣬����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE������BDA����AEC����BAC�����ж���DEF����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ȫУѧ����У��ѧ�ķ�ʽ����ȫУ�����ȡ��������ѧ�������ʾ����飮�ʾ�������������ѧ��ʽ��ѧ��ѡ��ÿ��ֻ��ѡһ��Ҳ��ܲ�ѡ��ͬʱ�ѵ���õ��Ľ�����Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ�������������������ͼ���ṩ����Ϣ����������⣺ 

��1������ε����У�һ����ȡ�˶�����ѧ����
��2��ͨ�����㲹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�������������������Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��4����ȫУ��1600��ѧ�������Ƹ�У����˽�ҳ���ѧ��ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
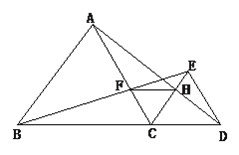
����Ŀ����ͼ����֪��B��C��D��ͬһ��ֱ���ϣ���ABC����CDE���ǵȱ�������.BE��AC��F��AD��CE��H��
����֤����BCE�ա�ACD��
����֤��CF=CH��
���ж���CFH����״��˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com