
【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
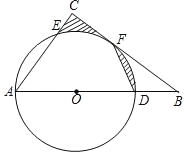
【答案】(1)证明详见解析;(2) 4.
【解析】
试题分析:(1)连接OF,AF,由题意得出![]() ,由圆周角定理和等腰三角形的性质得出∠1=∠3,证出AC∥OF,得出∠BFO=∠ACB=90°,即可得出结论;
,由圆周角定理和等腰三角形的性质得出∠1=∠3,证出AC∥OF,得出∠BFO=∠ACB=90°,即可得出结论;
(2)连接ED,交OF于H,由圆周角定理得出∠AED=90°,由勾股定理求出ED=8,证明四边形ECFH为矩形,得出∠EHO=90°,OF⊥ED,由三角形中位线定理得出OH=![]() =3,求出HF=5﹣3=2,得出
=3,求出HF=5﹣3=2,得出![]() =4,证出阴影部分的面积与△CEF的面积相等,即可得出答案.
=4,证出阴影部分的面积与△CEF的面积相等,即可得出答案.
试题解析:(1)连接OF,AF如图,
∵F为![]() 的中点,
的中点,
∴![]() ,
,
∴∠1=∠2,
∵AO=FO,
∴∠3=∠2,
∴∠1=∠3,
∴AC∥OF,
∴∠BFO=∠ACB=90°,
∵F为⊙O上一点,
∴BC为⊙O的切线;
(2)连接ED,交OF于H,如图,
∵AD为⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,ED=![]() =8,
=8,
∵∠AED=90°=∠ACF=∠BFO,
∴四边形ECFH为矩形,
∴∠EHO=90°,OF⊥ED,
∴H为ED的中点,
∴EH=4,
∵O为AD的中点,
∴OH=![]() =3,
=3,
∴HF=5﹣3=2,
∴![]() =4,
=4,
∵![]() ,
,
∴弓形FD与弓形EF全等,
∴阴影部分的面积与△CEF的面积相等,
故图中阴影部分的面积为4.


科目:初中数学 来源: 题型:
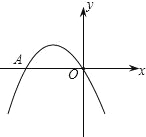
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).
(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2). 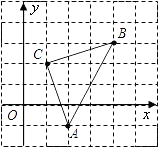
(1)写出点A,B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
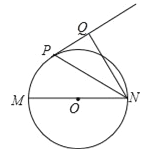
【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP=![]() ,求NQ的长.
,求NQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在6×4的正方形网格中,点A、B、C、D、E、F都在格点上.连接点A、B得线段AB.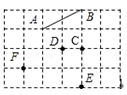
(1)连接C、D、E、F中的任意两点,共可得 条线段,在图中画出来;
(2)在(1)中所连得的线段中,与AB平行的线段是 ;
(3)用三角尺或量角器度量、检验,AB及(1)中所连得的线段中,互相垂直的线段有几对?(请用“⊥”表示出来) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店出售一种优惠卡,花200元买这种卡后,凭卡可以在这家商店按8折购物,下列情况买购物卡合算的是( )
A. 购物高于800元 B. 购物低于800元 C. 购物高于1 000元 D. 购物低于1 000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润为120元,为了扩大销量,尽快减少库存,超市准备适当降价,据测算,若每箱降价2元,则每天可多售出4箱.
(1)如果要使每天销售该饮料获利14000元,则每箱应降价多少元.
(2)每天销售该饮料获利能达到14500元吗?若能,则每箱应降价多少?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
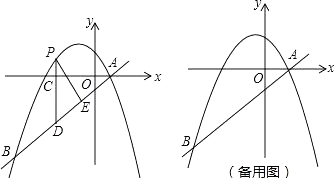
【题目】如图,在平面直角坐标系中,直线y=![]() 与抛物线y=
与抛物线y=![]() +bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com