
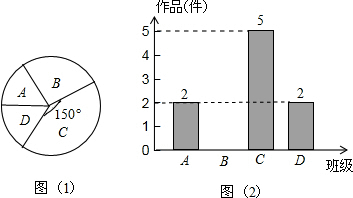
分析 (1)由全面调查和抽样调查的定义可知王老师采取的调查方式是抽样调查;由题意得:所调查的4个班征集到的作品数为:5÷$\frac{150}{360}$=12(件),B作品的件数为:12-2-5-2=3(件);继而可补全条形统计图;
(2)四个班平均每个班征集作品件数=总数÷4,全校作品总数=平均每个班征集作品件数×班级数;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中一男一女的情况,再利用概率公式即可求得答案.
解答 解:(1)王老师采取的调查方式是抽样调查;所调查的4个班征集到的作品数为:5÷$\frac{150}{360}$=12(件),B作品的件数为:12-2-5-2=3(件);
补全图2,如图所示:
(2)12÷4=3,3×14=42;
(3)画树状图得:
∵共有20种等可能的结果,恰好抽中一男一女的有12种情况,
∴恰好抽中一男一女的概率为:$\frac{12}{20}$=$\frac{2}{5}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -2和-0.5 | B. | -2和-1 | C. | -2和-1.5 | D. | -2和-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知线段AB,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,连接AC,BC,BD,CD.其中AB=4,CD=5,则四边形ABCD的面积为10.
如图,已知线段AB,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,连接AC,BC,BD,CD.其中AB=4,CD=5,则四边形ABCD的面积为10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
如图,有两棵树,一棵高10m,另一棵高5m,两树相距12m,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )| A. | 5m | B. | 10m | C. | 13m | D. | 17m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
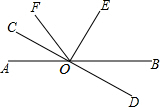 如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,
如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com