
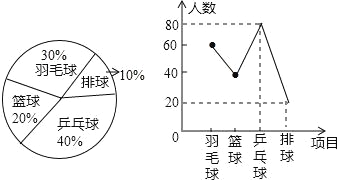
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.

(1)在这次调查活动中,一共调查了 名学生,并请补全统计图.
(2)“羽毛球”所在的扇形的圆心角是 度.
(3)若该校有学生1200名,估计爱好乒乓球运动的约有多少名学生?
【答案】(1)200,补图见解析;(2)108;(3)480.
【解析】
试题分析:(1)读图可知喜欢乒乓球的有80人,占40%.所以一共调查了80÷40%=200人;
(2)喜欢排球的20人,应占![]() ×100%=10%,喜欢羽毛球的应占统计图的1-20%-40%-10%=30%,所占的圆心角为360°×30%=108°;
×100%=10%,喜欢羽毛球的应占统计图的1-20%-40%-10%=30%,所占的圆心角为360°×30%=108°;
(3)利用样本估计总体的办法,计算出答案即可.
试题解析:(1)80÷40%=200(人)
喜欢篮球的人数:200×20%=40(人),
喜欢羽毛球的人数:200-80-20-40=60(人),
如图所示:
(2)![]() ×100%=10%,
×100%=10%,
1-20%-40%-10%=30%,
360°×30%=108°;
(3)喜欢乒乓球的人数:40%×1200=480(人).


科目:初中数学 来源: 题型:
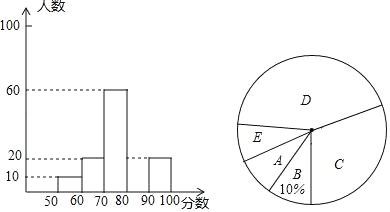
【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
(1)正比例函数![]() 过( 0 , )和( 1 , );
过( 0 , )和( 1 , );
(2)一次函数![]() ( 0 , )( , 0 ).
( 0 , )( , 0 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
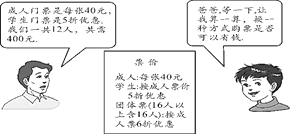
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某贸易公司购进“长青”胶州大白菜,进价为每棵20元,物价部门规定其销售单价每棵不得超过80元,也不得低于30元.经调查发现:日均销售量y(棵)与销售单价x(元/棵)满足一次函数关系,并且每棵售价60元时,日均销售90棵;每棵售价30元时,日均销售120棵.
(1)求日均销售量y与销售单价x的函数关系式;
(2)在销售过程中,每天还要支出其他费用200元,求销售利润w(元)与销售单价x之间的函数关系式;并求当销售单价为何值时,可获得最大的销售利润?最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠B、∠D的两边分别平行。

(1)在图①中,∠B与∠D的数量关系为相等相等。
(2)在图②中,∠B与∠D的数量关系为互补互补。
(3)用一句话归纳的结论为如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
试分别说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=![]() 时,求CG的长;
时,求CG的长;
(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com