
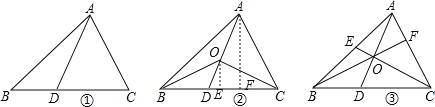
【题目】如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想![]() 的值,并说明理由.
的值,并说明理由.

【答案】(1)1:2,BD:BC;
(2)S△BOC:S△ABC=OD:AD,理由见解析;
(3)![]() =1,理由见解析.
=1,理由见解析.
【解析】
试题分析:(1)根据三角形的面积公式,两三角形等高时,可得两三角形底与面积的关系,可得答案;
(2)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,可得答案;
(3)根据三角形的面积公式,两三角形等底时,可得两三角形的高与面积的关系,再根据分式的加减,可得答案.
试题解析:(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC=1:2;当点D是BC边上任意一点时,S△ABD:S△ABC=BD:BC,
故答案为:1:2,BD:BC;
(2)S△BOC:S△ABC=OD:AD,
如图②作OE⊥BC与E,作AF⊥BC与F,,
∵OE∥AF,
∴△OED∽△AFD,
∴![]() .
.
∵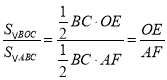 ,
,
∴![]() ;
;
(3)![]() =1,理由如下:
=1,理由如下:
由(2)得![]() ,
,![]() ,
,![]() .
.
∴![]() =
=![]() =
=![]() =1.
=1.
 .
.


科目:初中数学 来源: 题型:
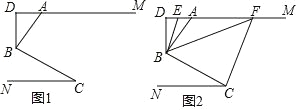
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…排列成如图所示的一个表.
(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x的式子表示出来,从大到小依次是 , , ;
(2)在(1)的前提下,当被框住的4个数之和等于984时,x位于该表的第几行第几列?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐篷;
(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.

(1)在这次调查活动中,一共调查了 名学生,并请补全统计图.
(2)“羽毛球”所在的扇形的圆心角是 度.
(3)若该校有学生1200名,估计爱好乒乓球运动的约有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(![]() ,0),如图所示:抛物线
,0),如图所示:抛物线![]() 经过点B。
经过点B。

(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com