【题目】以正方形
的边
为边作等边三角形
连接
则
的度数为______．
【答案】
或
【解析】
解答本题时要考虑两种情况，E点在正方形内和外两种情况，由正方形和等边三角形的性质容易得出结果．
解：如下图，当E点在正方形外部时，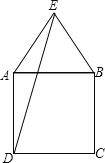
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵△ABE是等边三角形，
∴AE=AB，∠BAE=∠BEA=60°，
∴AD=AE，∠DAE=150°，
∴∠AED=∠ADE=
（180°-∠DAE）=15°，
∴∠DEB=∠BEA-∠AED=60°-15°=45°；
如下图，当E点在正方形内部时，
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵△ABE是等边三角形，
∴AE=AB，∠BAE=∠BEA=60°，
∴AD=AE，∠DAE=30°，
∴∠AED=∠ADE=（180°-∠DAE）=75°，
∴∠DEB=∠BEA+∠AED=60°+75°=135°．
综上所述∠DEB的度数为45°或135°，
故答案为：45°或135°．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．
问题引入：
（1）如图①，当点D是BC边上的中点时，S△ABD：S△ABC= ；当点D是BC边上任意一点时，S△ABD：S△ABC= （用图中已有线段表示）．
探索研究：
（2）如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．
拓展应用：
（3）如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想
的值，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠B、∠D的两边分别平行。
(1)在图①中，∠B与∠D的数量关系为相等相等。
(2)在图②中，∠B与∠D的数量关系为互补互补。
(3)用一句话归纳的结论为如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补如果一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补。
试分别说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC延长线于M，连接CD，下列四个结论：①∠ADC=45°；②BD=
AE；③AC+CE=AB；④AB-BC=2MC，其中正确的有（ ）个.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O是坐标原点，直线OA与双曲线
在第一象限内交于点A，过点A作AB⊥x轴，垂足为B，若OB=4，tan∠AOB=
．
（1）求双曲线的解析式；
（2）直线AC与y轴交于点C（0，1），与x轴交于点D，求D点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，
（1）求∠APO+∠DCO的度数；
（2）求证：AC=AO+AP.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．
（1）求证：△CDE≌△CBF；
（2）当DE=
时，求CG的长；
（3）连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.
（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到P1(1,1),第2次接着运动到点P2(2，0)，第3次接着运动到点P3(3，-2)，…，按这的运动规律,点P2019的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com