
分析 (1)设交点式,利用待定系数法求二次函数的解析式;
(2)化成一般式后,配方求顶点坐标.
解答 解:(1)∵A(-2,0)、B(1,0),
∴设抛物线的解析式为:y=a(x+2)(x-1),
把C(0,-4)代入得:-4=a(0+2)(0-1),
a=2,
∴抛物线的解析式为:y=2(x+2)(x-1)=2x2+2x-4;
(2)y=2x2+2x-4=2(x2+x+$\frac{1}{4}$-$\frac{1}{4}$)-4=2(x+$\frac{1}{2}$)2-4.5;
∴顶点坐标为(-$\frac{1}{2}$,-4.5).
点评 本题考查了利用待定系数法求二次函数的解析式、抛物线的顶点坐标;难度不大,求抛物线的顶点坐标时,可以配方成顶点式或利用顶点坐标公式(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)来求.


科目:初中数学 来源: 题型:解答题
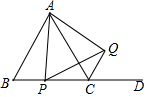 如图,△ABC是等边三角形,AB=2,动点P从点B出发,以1cm/s速度沿射线BC运动,连接AP,以AP为边向其右侧作等边三角形APQ,连按CQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=2,动点P从点B出发,以1cm/s速度沿射线BC运动,连接AP,以AP为边向其右侧作等边三角形APQ,连按CQ,设点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com