
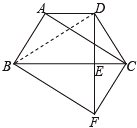
【题目】如图,在梯形![]() ,
,![]() ,过点
,过点![]() ,垂足为
,垂足为![]() ,并延长
,并延长![]() ,使
,使![]() ,联结
,联结![]() .
.
(1)求证:四边形![]() 是平行四边形。
是平行四边形。
(2)联结![]() ,如果
,如果![]()

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接BD,证△ABC≌△DCB,得∠ACB=∠DBC.由中垂线性质得BD=BF,∠DBC=∠FBC,
再证得AC=BF,∠ACB=∠CBF,由AC,BF平行且相等可证得四边形![]() 是平行四边形.
是平行四边形.
(2)由BF=DF=BD证得三角形BDF是等边三角形,可得![]() ,再由平行线性质和等腰三角形性质证
,再由平行线性质和等腰三角形性质证![]() ,可得
,可得![]() ,由(1)可得
,由(1)可得![]()
∵梯形ABCD中,AD∥BC,AB=DC,
∴AC=BD,
∵△ABC和△DCB中,AB=DC,AC=BD,BC=CB,
∴△ABC≌△DCB.
∴∠ACB=∠DBC.
又∵DE⊥BC,EF=DE,
∴BD=BF,∠DBC=∠FBC,
∴AC=BF,∠ACB=∠CBF,
∴AC∥BF,
∴四边形ABFC是平行四边形;
(2)
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 四边形ABFC是平行四边形
四边形ABFC是平行四边形
![]()


科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论; 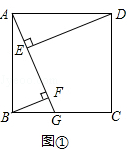
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系; 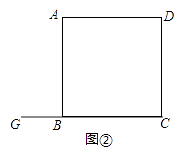
(3)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由. 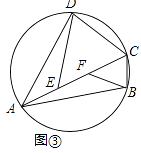
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车间共120人,其中甲车间人数比乙车间人数的4倍少5人.
(1)求甲、乙两车间各有多少人?
(2)若从甲、乙两车间分别抽调工人,组成丙车间研制新产品,并使甲、乙、丙三个车间的人数比为13∶4∶7,那么甲、乙两车间要分别抽调多少工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期天下午,小强和同学小颖相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小颖到了后两人一起乘公共汽车回学校,图中折线表示小强离开家的路程y(公里)和所用时间x(分)之间的函数关系,下列说法中错误的是( )
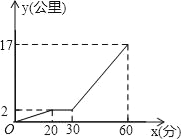
A. 小强乘公共汽车用了20分钟 B. 小强在公共汽车站等小颖用了10分钟
C. 公共汽车的平均速度是30公里/小时 D. 小强从家到公共汽车站步行了2公里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
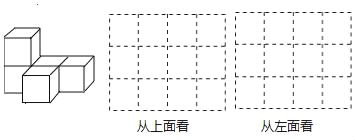
【题目】由大小相同的小立方块搭成的几何体如左图:
(1)请在下面的方格中画出该几何体从上面和从左面看的两个图形.
(2)若现在你手头上还有一些相同的小立方块,如果保持从上面看和从左面看所得图形不变,则在左图中最多可以再添加 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(-1,1),(0,0)和(1,0).
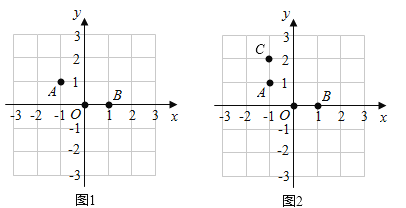
(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表: 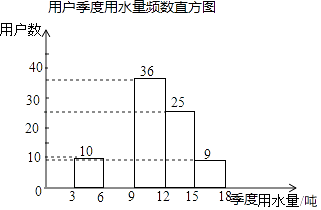
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= , n=;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com