
���� ��1�����������ľ��빫ʽ֤�����ɣ�
��2������ȷ������P�ڹ���C��ֱ��x��������ߵĽ��㣬���ã�1���Ľ����������
�����������ε���������P��ֱ�߽���ʽ���Ӷ������P���꣬���ã�1���Ľ����������
��� �⣺��1���ߵ�P��m��n����PB��x�ᣬ����ΪB��
��PB=|n|=-n��
�ߵ�P��m��n����������y=-$\frac{1}{6}$x2-$\frac{3}{2}$�ϵ�һ�����㣬
��n=-$\frac{1}{6}$m2-$\frac{3}{2}$��
��m2=-6n-9��
��A��0��-3����P��m��n��
��PA=$\sqrt{{m}^{2}+��n+3��^{2}}$=$\sqrt{-6n-9+{n}^{2}+6n+9}$=$\sqrt{{n}^{2}}$=|n|=-n��
��PA=PB��
�ʴ�Ϊ��=
��2���ٴ��ڣ�
��ͼ����CD��x�ᣬ
��A��0��-3����C��2��-5����
��AC=2$\sqrt{2}$��CD=5��
���APC���ܳ�=AC+PC+PA=2$\sqrt{2}$+PC+PA
�ߡ�APC���ܳ���С��
��PC+PA����
�ɣ�1���У���P��x��ľ�����ڵ�P����A�ľ��룬
���P��CD�ϣ�
��PC+PA=CD=5��
���APC���ܳ���СֵΪ2$\sqrt{2}$+5��
�ߵ�P��CD�ϣ�
��m=2��
��n=-$\frac{1}{6}$m2-$\frac{3}{2}$=-$\frac{13}{6}$��
��P��2��-$\frac{13}{6}$����
����ͼ��
����C��CE��y�ᣬ
��CE=2��
��A��0��-3����E��0��-5����
��AE=2��
���CAE=45��
��ACƽ������ƽ�ƣ���y����F��
����F��FD��AC��D��
���DAF=45�㣬
��Rt��ADF��sin��DAF=$\frac{DF}{AF}$=$\frac{CE}{AC}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$��
��AF=$\sqrt{2}$DF��
��AC=2$\sqrt{2}$����APC���������$\frac{3}{2}$��
���P��ֱ��AC�ľ���h=$\frac{3\sqrt{2}}{4}$��
��AF=$\sqrt{2}$h=$\frac{3}{2}$��
��A��0��-3����C��2��-5����
��ֱ��AC����ʽΪy=-x-3��
�����Pƽ����AC��ֱ��l����ʽΪy=-x-3-$\frac{3}{2}$�ٻ�y=-x-3+$\frac{3}{2}$��
�������߽���ʽΪy=-$\frac{1}{6}$x2-$\frac{3}{2}$�ۣ�
�����٢ۣ���� $\left\{\begin{array}{l}{x=3+3\sqrt{3}}\\{y=-��\frac{15}{2}-3\sqrt{3}��}\end{array}\right.$�� $\left\{\begin{array}{l}{x=3-3\sqrt{3}}\\{y=\frac{15}{2}+3\sqrt{3}}\end{array}\right.$$\left\{\begin{array}{l}{x=3-3\sqrt{3}}\\{y=-��\frac{15}{2}+3\sqrt{3}��}\end{array}\right.$��
�ɣ�1�����ۣ��ã�PA=-y=$\frac{15}{2}$-3$\sqrt{3}$��$\frac{15}{2}$+3$\sqrt{3}$��
�����ڢۣ��ⷽ�����y=-$\frac{3}{2}$��y=-$\frac{15}{2}$��
��PA=$\frac{3}{2}$��$\frac{15}{2}$��
����PA�ij�Ϊ$\frac{15}{2}$-3$\sqrt{3}$��$\frac{15}{2}$+3$\sqrt{3}$��$\frac{3}{2}$��$\frac{15}{2}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����������ľ��빫ʽ��ͼ��Ľ��������ȷ������������ļ��㣬�Ȿ��Ĺؼ��ǻ��ã�1���Ľ��۽�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-2 | B�� | x��-2 | C�� | -2��x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
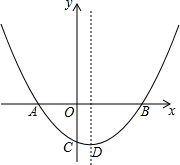 ��ͼ��������y=ax2+bx-1��a��0������A��-1��0����B��2��0�����㣬��y�ύ�ڵ�C��
��ͼ��������y=ax2+bx-1��a��0������A��-1��0����B��2��0�����㣬��y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��x+y��=ax+ay | B�� | x2-4x+4=��x-2��2 | ||
| C�� | 2a-4b+2=2��a-2b�� | D�� | x2-16+3x=��x-4����x+4��+3x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{\frac{1}{2}}$ | C�� | $\sqrt{12}$ | D�� | $\sqrt{18}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com