
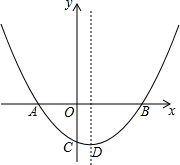
 如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.分析 (1)利用待定系数法求出抛物线解析式;
(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可.
(3)作出辅助线,利用tan∠MDN=2或$\frac{1}{2}$,建立关于点N的横坐标的方程,求出即可.
解答 解:(1)∵抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,
∴$\left\{\begin{array}{l}{a-b-1=0}\\{4a+2b-1=0}\end{array}\right.$
∴$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴抛物线解析式为y=$\frac{1}{2}$x2-$\frac{1}{2}$x-1=$\frac{1}{2}$(x-$\frac{1}{2}$)2-$\frac{9}{8}$,
∴抛物线的顶点坐标为($\frac{1}{2}$,-$\frac{9}{8}$),
(2)如图1,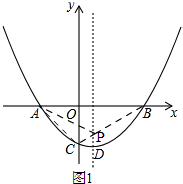
连接BC与抛物线对称轴的交点就是点P,连接AC,AP,
∵点A,B关于抛物线对称轴对称,
∴PA=PB,
∵B(2,0),C(0,-1),
∴直线BC解析式为y=$\frac{1}{2}$x-1,
∵点P在抛物线对称轴上,
∴点P的横坐标为$\frac{1}{2}$,
∴点P的纵坐标为-$\frac{3}{4}$,
∴P($\frac{1}{2}$,-$\frac{3}{4}$),
(3)如图2,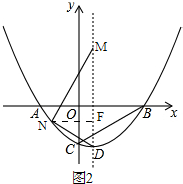
过点作NF⊥DM,
∵B(2,0),C(0,-1),
∴OB=2,OC=1,
∴tan∠OBC=$\frac{OC}{OB}$=$\frac{1}{2}$,tan∠OCB=$\frac{OB}{OC}$=2,
设点N(m,$\frac{1}{2}$m2-$\frac{1}{2}$m-1),
∴FN=|m-$\frac{1}{2}$|,FD=|$\frac{1}{2}$m2-$\frac{1}{2}$m-1+$\frac{9}{8}$|=|$\frac{1}{2}$m2-$\frac{1}{2}$m+$\frac{1}{8}$|,
∵Rt△DNM与Rt△BOC相似,
∴∠MDN=∠OBC,或∠MDN=∠OCB,
①当∠MDN=∠OBC时,
∴tan∠MDN=$\frac{FN}{FD}$=$\frac{1}{2}$,
∴$\frac{|m-\frac{1}{2}|}{|\frac{1}{2}{m}^{2}-\frac{1}{2}m+\frac{1}{8}|}$=$\frac{1}{2}$
∴m=$\frac{1}{2}$(舍)或m=$\frac{9}{2}$或m=-$\frac{7}{2}$,
∴N($\frac{9}{2}$,$\frac{55}{8}$)或(-$\frac{7}{2}$,$\frac{55}{8}$),
②当∠MDN=∠OCB时,
∴tan∠MDN=$\frac{FN}{FD}$=2,
∴$\frac{|m-\frac{1}{2}|}{|\frac{1}{2}{m}^{2}-\frac{1}{2}m+\frac{1}{8}|}$=2,
∴m=$\frac{1}{2}$(舍)或m=$\frac{3}{2}$或m=-$\frac{1}{2}$,
∴N($\frac{3}{2}$,-$\frac{5}{8}$)或(-$\frac{1}{2}$,-$\frac{5}{8}$);
∴符合条件的点N的坐标($\frac{9}{2}$,$\frac{55}{8}$)或(-$\frac{7}{2}$,$\frac{55}{8}$)或($\frac{3}{2}$,-$\frac{5}{8}$)或(-$\frac{1}{2}$,-$\frac{5}{8}$).
点评 此题是二次函数综合题,主要考查了待定系数法,抛物线的对称性,三角函数,三角形周长的计算,绝对值方程,过点N作抛物线对称轴的垂线是解本题的关键也是难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 8元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3天内会下雨 | |
| B. | 367人中至少有2人公历生日相同 | |
| C. | 打开电视,正在播放广告 | |
| D. | 某妇产医院里,下一个出生的婴儿是女孩 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 为了解我校初中学生对球类活动的喜爱情况,随机抽查了40名初中学生,让每人选一项自己喜欢的球类运动,并制成如图所示的扇形统计图.已知我校有200名初中学生,则喜爱乒乓球的学生约有30人.
为了解我校初中学生对球类活动的喜爱情况,随机抽查了40名初中学生,让每人选一项自己喜欢的球类运动,并制成如图所示的扇形统计图.已知我校有200名初中学生,则喜爱乒乓球的学生约有30人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点E、F是四边形ABCD的边AD、BC上的点,连接EF,将四边形ABFE沿直线EF折叠,若点A,点B都落在四边形ABCD内部,记∠C+∠D=a,则下列结论一定正确的是( )
如图,点E、F是四边形ABCD的边AD、BC上的点,连接EF,将四边形ABFE沿直线EF折叠,若点A,点B都落在四边形ABCD内部,记∠C+∠D=a,则下列结论一定正确的是( )| A. | ∠1+∠2=180°-α | B. | ∠1+∠2=360°-α | C. | ∠1+∠2=360°-2α | D. | ∠1+∠2=540°-2α |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )
如图,E是正方形ABCD的边BC延长线上的一点,且CE=CA,AE交CD于点F,则∠DAF的度数为( )| A. | 45° | B. | 30° | C. | 20° | D. | 22.5° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com