
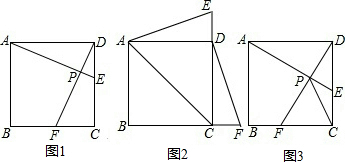
���� ��1�����������ε����ʵó�AD=DC����ADE=��DCF=90�㣬���DE=CF������SAS�Ƴ���ADE�ա�DCF������ȫ�������ε����ʵó�AE=DF����DAE=��FDC���ɣ�
��2��������������ٵ�AC=CEʱ����������ABCD�ı߳�Ϊa���ɹ��ɶ������AC=CE=$\sqrt{2}$a���ɣ��ڵ�AE=ACʱ����������ABCD�ı߳�Ϊa���ɹ��ɶ������AC=AE=$\sqrt{2}$a�����������ε����ʡ�ADC=90�㣬���ݵ��������ε����ʵó�DE=CD=a���ɣ�
��3�����ݣ�1����2��֪����P���˶��б��֡�APD=90�㣬�ó���P��·������ADΪֱ����Բ����AD���е�ΪQ������CQ���ӳ���Բ���ڵ�P����ʱCP�ij���������QC���ɣ�
��� �⣺��1��AE=DF��AE��DF��
�����ǣ����ı���ABCD�������Σ�
��AD=DC����ADE=��DCF=90�㣬
�߶���E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ���
��DE=CF��
�ڡ�ADE�͡�DCF��
$\left\{\begin{array}{l}{AD=DC}\\{��ADE=��DCF}\\{DE=CF}\end{array}\right.$��
���ADE�ա�DCF��
��AE=DF����DAE=��FDC��
�ߡ�ADE=90�㣬
���ADP+��CDF=90�㣬
���ADP+��DAE=90�㣬
���APD=180��-90��=90�㣬
��AE��DF��
��2��

��1���еĽ��ۻ�������CE��CD=$\sqrt{2}$��2��
�����ǣ������������
����ͼ1����AC=CEʱ��
��������ABCD�ı߳�Ϊa���ɹ��ɶ����ã�AC=CE=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a��
��CE��CD=$\sqrt{2}$a��a=$\sqrt{2}$��
����ͼ2����AE=ACʱ��
��������ABCD�ı߳�Ϊa���ɹ��ɶ����ã�AC=AE=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a��
���ı���ABCD�������Σ�
���ADC=90�㣬��AD��CE��
��DE=CD=a��
��CE��CD=2a��a=2��
��CE��CD=$\sqrt{2}$��2��
��3���ߵ�P���˶��б��֡�APD=90�㣬
���P��·������ADΪֱ����Բ��
��ͼ3����AD���е�ΪQ������CQ���ӳ���Բ���ڵ�P����ʱCP�ij������
����Rt��QDC��QC=$\sqrt{C{D}^{2}+Q{D}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��
��CP=QC+QP=$\sqrt{5}$+1��
���߶�CP�����ֵ��$\sqrt{5}$+1��
���� ���⿼���������ε����ʣ����ɶ�����Բ�ܽǶ�����ȫ�������ε����ʺ��ж������������ε����ʣ������ε��ڽǺͶ�����Ӧ�ã����ۺ��������ʽ��������ǽ����Ĺؼ������˷�������˼�룬�Ѷ�ƫ��


 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
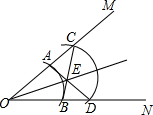 ��λͬѧ�����ˡ���ƽ���ߡ�����һ�ֳ߹��������䷽��Ϊ��
��λͬѧ�����ˡ���ƽ���ߡ�����һ�ֳ߹��������䷽��Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
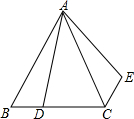 ��ͼ���ڵȱ�������ABC�У�AB=6��D��BC��һ�㣬��BC=3BD����ABD�Ƶ�A��ת��õ���ACE����CE�ij���Ϊ��������
��ͼ���ڵȱ�������ABC�У�AB=6��D��BC��һ�㣬��BC=3BD����ABD�Ƶ�A��ת��õ���ACE����CE�ij���Ϊ��������| A�� | 6 | B�� | 5 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
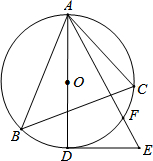 ��ͼ����֪��ABC�ǡ�O��Բ�ڽ������Σ�ADΪ��O��ֱ����DEΪ��O�����ߣ�AE����O�ڵ�F����C=��E��
��ͼ����֪��ABC�ǡ�O��Բ�ڽ������Σ�ADΪ��O��ֱ����DEΪ��O�����ߣ�AE����O�ڵ�F����C=��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
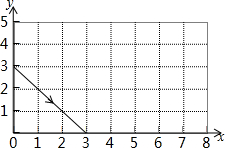 ��ͼ��һ���Դ�ڣ�0��3����������ʾ�ķ����䣬�����������������ĸ�ƽ�澵��������ƽ�洹ֱ���ã����һ�������P1����Ϊ��3��0������ڶ��������P2��6��3���������������P3��3��6����������·ͼ����д����2013�������P2013��3��0��
��ͼ��һ���Դ�ڣ�0��3����������ʾ�ķ����䣬�����������������ĸ�ƽ�澵��������ƽ�洹ֱ���ã����һ�������P1����Ϊ��3��0������ڶ��������P2��6��3���������������P3��3��6����������·ͼ����д����2013�������P2013��3��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com