练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若方程x2-2x-2014=0的两根为a，b，则a2-3a-b的值为2012．

    分析 首先根据方程x2-2x-2014=0的两根为a，b，求出a+b=2，a2-2a=2014，然后整体代值计算．

    解答 解：∵方程x2-2x-2014=0的两根为a，b，
    ∴a+b=2，a2-2a=2014，
    ∴a2-3a-b=（a2-2a）-（a+b）=2014-2=2012，
    故答案为2012．

    点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了一元二次方程的解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．某市为鼓励市民节约用水和加强对节水的管理，制定了以下每月每户用水的收费标准：
    ①用水量不超过8立方米时，每立方米收费0.8元，并加收每立方米0.2元的污水处理费；
    ②用水量超过8立方米时，在①的基础上，超过8立方米的部分，每立方米收费1.6元，并加收每立方米0.4元的污水处理费．
    设某户一个月的用水量为x立方米，应交水费为y元
    （1）试分析对①②两种情况，求出y关于x的函数解析式，并写出函数的定义域；
    （2）如果该户一个月的水费为20元，求该户这一个月的用水量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动．
    （1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的数量关系和位置关系，并说明理由；
    （2）如图2，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，请你直接写出△ACE为等腰三角形时CE：CD的值；
    （3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请你画出点P运动路径的草图．若AD=2，试求出线段CP的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知y1=2x-3，y2=-x+3，当x取何值时，
    （1）y1≤y2；                 
    （2）y1＞y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知关于x的方程x2-4x+3=0的两个根是m和n，则mn=3，m+n=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

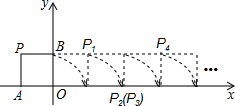    4．如图，将边长为1的正方形OAPB沿x轴正方向连续翻转2003次，点P依次落在点P1、P2、P3、P4…Pn的位置，则P2003的横坐标x2003=2002．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

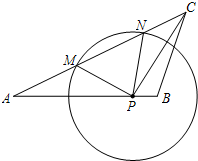    11．如图，已知在△ABC中，AB=15，AC=20，tanA=$\frac{1}{2}$，点P在AB边上，⊙P的半径为定长．当点P与点B重合时，⊙P恰好与AC边相切；当点P与点B不重合时，⊙P与AC边相交于点M和点N．
    （1）求⊙P的半径；
    （2）当AP=$6\sqrt{5}$时，试探究△APM与△PCN是否相似，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

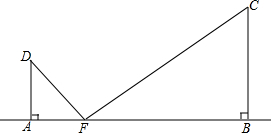    8．一条宽阔的街道的两侧有两个建筑物AD和BC，王洋在街道的两建筑物之间测AD的仰角为45°，建筑物BC的仰角为57°，已知两建筑物的高度之和为60米，两街道宽AB=50米，求建筑物BC的高度．（sin57°≈0.83，cos57°≈0.54，tan57≈1.5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．在△ABC中，∠BAC=90°，∠C=30°，BC=6，P为直线AC上的一点（不与A、C重合），满足∠APB=60°，则CP=4$\sqrt{3}$或2$\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案