
【题目】如图,已知等边三角形ABC的边长为2,E、F、G分别是边AB、BC、CA的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y与x的函数图象大致是( )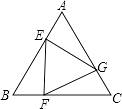
A.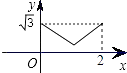
B.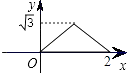
C.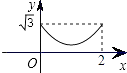
D.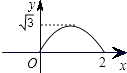
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数![]() 的图象经过点E,G两点,则k的值为 ______________.
的图象经过点E,G两点,则k的值为 ______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
门头沟盛产名特果品,东山的京白梨,灵水的核桃,柏峪的扁杏仁,龙泉雾的香白杏,火村红杏,太子墓的红富士苹果,陇驾庄盖柿都是上等的干鲜果品,有的曾为皇宫供品,至今在国内享有盛名.秋收季节,某公司打算到门头沟果园基地购买一批优质苹果.果园基地对购买量在1000千克(含1000千克)以上的有两种销售方案,方案一:每千克10元,由基地送货上门;方案二:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.
(1)公司购买多少千克苹果时,选择两种购买方案的付款费用相同;
(2)如果公司打算购买3000千克苹果,选择哪种方案付款最少?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=![]() 的下列说法正确的是( )
的下列说法正确的是( )
① 该函数的图象在第二、四象限;
② A(x1、y1)、B(x2、y2)两点在该函数图象上,若x1<x2,则y1<y2;
③ 当x>2时,则y>-2;
④ 若反比例函数y=![]() 与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
与一次函数y=x+b的图象无交点,则b的范围是-4<b<4.
A. ① ③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程x2-(2k+1)x+4k-2=0
的方程x2-(2k+1)x+4k-2=0
(1)求证:不论k取何值,这个方程总有实数根
(2)若等腰△ABC一边长a=4,另两边长b,c恰好是这个方程的两根,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com