
【题目】已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF,M为EF的中点,则CM的最小值为 .
【答案】1.2
【解析】解:如图,连接CP. ∵AC=3,BC=4,AB=5
∴∠ACB=90°,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFPE是矩形,
∴EF=CP,
由垂线段最短可得CP⊥AB时,线段EF的值最小,则CM最小,
此时,S△ABC= ![]() BCAC=
BCAC= ![]() ABCP,
ABCP,
即 ![]() ×4×3=
×4×3= ![]() ×5CP,
×5CP,
解得CP=2.4.
∴EF=2.4,
∵M为EF中点,
∴CM=1.2
故答案为:1.2.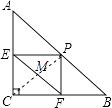
连接CP,利用勾股定理逆定理可得∠ACB=90°,判断出四边形CFPE是矩形,根据矩形的对角线相等可得EF=CP,再根据垂线段最短可得CP⊥AB时,线段EF的值最小,则CM最小,然后根据三角形的面积公式列出方程求解即可.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
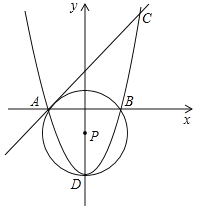
【题目】(14分)在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,5).
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题(2)利用乘法分配律及去括号法则先去括号,然后再合并同类项即可;
(1)计算 ![]()
![]()
(2)化简 ![]()
(3)解方程 ![]()
(4)先化简,再求值 ![]() ,其中a=2,b=-1
,其中a=2,b=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列说法中是错误的是( )
A.在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形
B.在△ABC中,∠C=∠A﹣∠B,则△ABC为直角三角形
C.在△ABC中,若a= ![]() c,b=
c,b= ![]() c,则△ABC为直角三角形
c,则△ABC为直角三角形
D.在△ABC中,若a:b:c=2:2:4,则△ABC为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船航行到C处观测小岛A的方向是北偏西54°,那么从A同时观测轮船在C处的方向是( )
A. 南偏东54° B. 东偏北36° C. 东偏南54° D. 南偏东36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣ ![]() |+
|+ ![]() +(c﹣4
+(c﹣4 ![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2). 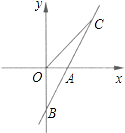
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com