
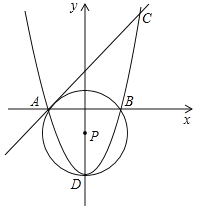
【题目】(14分)在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,5).
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
【答案】(1)y=x+2,![]() ;(2)P(0,
;(2)P(0,![]() );(3)Q(
);(3)Q(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用抛物线和x轴的两个交点坐标,设出抛物线的解析式![]() ,代入即可得出抛物线的解析式,再设出直线AC的解析式,利用待定系数法即可得出答案;
,代入即可得出抛物线的解析式,再设出直线AC的解析式,利用待定系数法即可得出答案;
(2)先求得抛物线的顶点D的坐标,再设点P坐标(0,Py),根据A,B,D三点在⊙P上,得PB=PD,列出关于Py的方程,求解即可得出P点的坐标;
(3)假设抛物线上存在这样的点Q使直线AQ与⊙P相切,设Q点的坐标为(m,m2﹣4),根据平面内两点间的距离公式,即可得出关于m的方程,求出m的值,即可得出点Q的坐标.
试题解析:(1)∵A(﹣2,0),B(2,0);
∴设二次函数的解析式为y=a(x﹣2)(x+2)…①,把C(3,5)代入①得a=1;
∴二次函数的解析式为:![]() ;
;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(﹣2,0),C(3,5)代入②得:![]() ,解得:
,解得:![]() ,∴一次函数的解析式为:y=x+2;
,∴一次函数的解析式为:y=x+2;
(2)设P点的坐标为(0,![]() ),由(1)知D点的坐标为(0,﹣4);
),由(1)知D点的坐标为(0,﹣4);
∵A,B,D三点在⊙P上,∴PB=PD,∴![]() ,解得:
,解得:![]() =
=![]() ,∴P点的坐标为(0,
,∴P点的坐标为(0,![]() );
);
(3)在抛物线上存在这样的点Q使直线AQ与⊙P相切.
理由如下:设Q点的坐标为(m,![]() ),根据平面内两点间的距离公式得:
),根据平面内两点间的距离公式得:![]() =
=![]() ,
,![]() =
=![]() ;
;
∵AP=![]() ,∴
,∴![]() =
=![]() ;
;
∵直线AQ是⊙P的切线,∴AP⊥AQ;
∴![]() ,即:
,即:![]() =
=![]() +
+![]() ,解得:
,解得:![]() =
=![]() ,
,![]() =﹣2(与A点重合,舍去),∴Q点的坐标为(
=﹣2(与A点重合,舍去),∴Q点的坐标为(![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:

(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
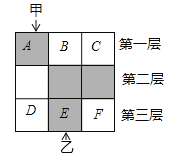
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列顺序排列的等式:9 ![]() 0+1=1,9
0+1=1,9 ![]() 1+2=11,9
1+2=11,9 ![]() 2+3=21,9
2+3=21,9 ![]() 3+4=31,9
3+4=31,9 ![]() +5=41,……
+5=41,……
根据以上所反映的规律,猜想,第n个等式(n为正整数)应为( )
A.9(n-1)+n=10(n-1)+1
B.9n+n=(n-1)+n
C.9n+(n-1)=n2 -1
D.9n+n=10n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个算式:(1)(x4)4=x4+4=x8;(2)[(y2)2]2=y2×2×2=y8;(3)(﹣y2)3=y6;(4)[(﹣x)3]2=(﹣x)6=x6 .
其中正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AC=3,BC=4,AB=5,点P在AB上(不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF,M为EF的中点,则CM的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国一些地区遭受旱灾,旱灾牵动全国人民的心.图(1)是我市某中学“献爱心,抗旱灾”自愿捐款活动中学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1450人).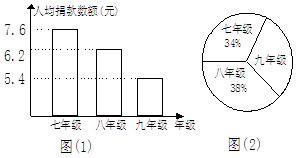
(1)初三学生共捐款多少元?
(2)该校学生平均每人捐款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com