
【题目】邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与研究:
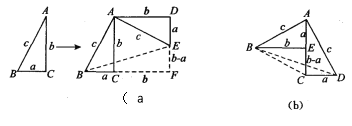
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
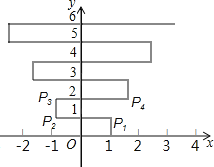
【题目】如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是 ,点P第8次跳动至P8的坐标为 ;则点P第256次跳动至P256的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是方程x2﹣2x﹣1=0的两根,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于( )
A.﹣5 B.5 C.﹣9 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com