
【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2![]() ,则阴影部分图形的面积为( )
,则阴影部分图形的面积为( )
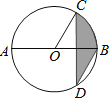
A.4π B.2π C.π D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码记忆方便.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式x3﹣xy2,取x=20,y=10,用上述方法产生的密码不可能是( )
A.201010 B.203010 C.301020 D.201030
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.
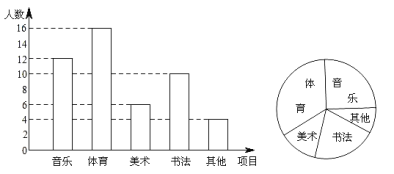
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
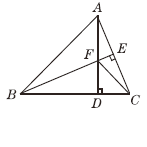
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
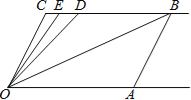
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
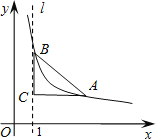
【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数![]() 的图象上.那么k的值是 .
的图象上.那么k的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
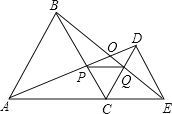
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
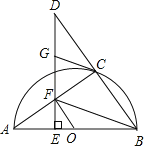
(1)求证:CG是⊙O的切线;
(2)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com