Question

【题目】如图，点C在以AB为直径的半圆O上，延长BC到点D，使得CD=BC，过点D作DE⊥AB于点E，交AC于点F，点G为DF的中点，连接CG、OF、FB．

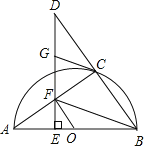
（1）求证：CG是⊙O的切线；

（2）若△AFB的面积是△DCG的面积的2倍，求证：OF∥BC．

Answer 1

【答案】见解析

【解析】

试题分析：（1）连接OC．欲证CG是⊙O的切线，只需证明∠CGO=90°，即CG⊥OC；

（2）根据直角三角形ABC、直角三角形DCF的面积公式，以及直角三角形斜边的中线等于斜边的一半求得AC=2AF；然后根据三角形中位线的判定与定理证得该结论．

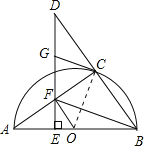
证明：（1）如图，连接OC．

在△ABC中，∵AB是⊙O的直径，

∴∠ACB=90°（直径所对的圆周角是直角）；

又∵OA=OC，

∴∠A=∠ACO（等边对等角）；

在Rt△DCF中，∵点G为DF的中点，∴CG=GF（直角三角形斜边上的中线是斜边的一半），

∴∠GCF=∠CFG（等边对等角）；

∵DE⊥AB（已知），∠CFG=∠AFE（对顶角相等）；

∴在Rt△AEF中，∠A+∠AFE=90°；

∴∠ACO+∠GCF=90°，即∠GCO=90°，

∴CG⊥OC，

∴CG是⊙O的切线；

（2）∵AB是⊙O的直径，

∴∠ACB=90°（直径所对的圆周角是直角），即AC⊥BD；

又∵CD=BC，点G为DF的中点，

∴S△AFB=S△ABC﹣S△BCF=（ACBC﹣CFBC），S△DCG=S△FCD=×DCCF=BCCF；

∵△AFB的面积是△DCG的面积的2倍，

∴（ACBC﹣CFBC）=2×BCCF，

∴AC=2CF，即点F是AC的中点；

∵O点是AB的中点，

∴OF是△ABC的中位线，

∴OF∥BC．