
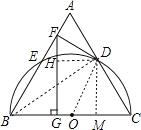
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为 .

【答案】3![]()
【解析】
试题分析:连结OD,作DH⊥FG于H,DM⊥BC于M,根据等边三角形的性质得∠A=∠C=∠ABC=60°,AC=BC,根据切线的性质得OD⊥DF,再证明OD∥AB,则DF⊥AB,在Rt△ADF中根据含30度的直角三角形三边的关系得DF=![]() AF=2
AF=2![]() ,由BC为⊙O的直径,根据圆周角定理得∠BDC=90°,则AD=CD=4,OD=4,所以OM=
,由BC为⊙O的直径,根据圆周角定理得∠BDC=90°,则AD=CD=4,OD=4,所以OM=![]() OD=2,在Rt△DFH中可计算出FH=
OD=2,在Rt△DFH中可计算出FH=![]() ,DH=
,DH=![]() FH=3,则GM=3,于是OG=GM﹣OM=1,BG=OB﹣OG=3,在Rt△BGF中可计算FG=
FH=3,则GM=3,于是OG=GM﹣OM=1,BG=OB﹣OG=3,在Rt△BGF中可计算FG=![]() BG=3
BG=3![]() .
.
解:连结OD,作DH⊥FG于H,DM⊥BC于M,如图,
∵△ABC为等边三角形,
∴∠A=∠C=∠ABC=60°,AC=BC,
∵DF是圆的切线,
∴OD⊥DF,
∵△ODC为等边三角形,
∴∠ODC=60°,
∴∠A=∠ODC,
∴OD∥AB,
∴DF⊥AB,
在Rt△ADF中,AF=2,∠A=60°,
∴AD=4,DF=![]() AF=2
AF=2![]() ,
,
∵BC为⊙O的直径,
∴∠BDC=90°,
∴BD⊥AC,
∴AD=CD=4,
∴OD=4,
∴OM=![]() OD=2,
OD=2,
在Rt△DFH中,∠DFH=60°,DF=2![]() ,
,
∴FH=![]() ,DH=
,DH=![]() FH=3,
FH=3,
∴GM=3,
∴OG=GM﹣OM=1,
∴BG=OB﹣OG=3,
在Rt△BGF中,∠FBG=60°,BG=3,
∴FG=![]() BG=3
BG=3![]() .
.
故答案为3![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
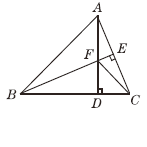
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
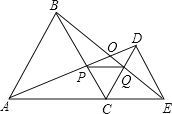
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠1与∠2是一组平行线被第三条直线所截的同旁内角,若∠1=50°,则( )
A. ∠2=50° B. ∠2=130° C. ∠2=50°或∠2=130° D. ∠2的大小不一定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,
①若AB=BC=CA,则△ABC为等边三角形;
②若∠A=∠B=∠C,则△ABC为等边三角形;
③有两个角都是60°的三角形是等边三角形;
④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
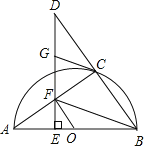
(1)求证:CG是⊙O的切线;
(2)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑶海教育局计划在3月12日植树节当天安排A,B两校部分学生到郊区公园参加植树活动.已知A校区的每位学生往返车费是6元,B校每位学生的往返车费是10元,要求两所学校均要有学生参加,且A校参加活动的学生比B校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求A,B两校最多各有多少学生参加?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com