
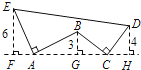
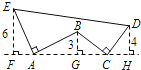
【题目】如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 .
【答案】50.
【解析】
试题分析:由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≌△ABG,所以AF=BG,AG=EF;同理证得△BGC≌△DHC,GC=DH,CH=BG,故FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH∠FED=∠EFA=∠BGA=90°,
∠EAF+∠BAG=90°,∠ABG+∠BAG=90°∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG△EFA≌△ABG
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=![]() (6+4)×16﹣3×4﹣6×3=50.
(6+4)×16﹣3×4﹣6×3=50.
故答案为50.


科目:初中数学 来源: 题型:
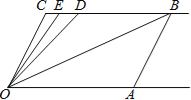
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内有直线a1,a2,a3,a4, …, a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5, …,按此规律进行下去,则a1与a100的位置关系是( )
A. 平行 B. 相交 C. 重合 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,
①若AB=BC=CA,则△ABC为等边三角形;
②若∠A=∠B=∠C,则△ABC为等边三角形;
③有两个角都是60°的三角形是等边三角形;
④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
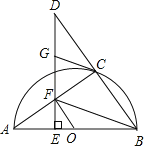
【题目】如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(1)求证:CG是⊙O的切线;
(2)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
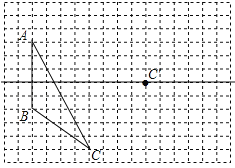
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是 ;
(3)利用网格画出△ABC 中AC边上的中线BD;
(4)利用网格画出△ABC 中AB边上的高CE;
(5)△A′B′C′的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com