
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸中将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
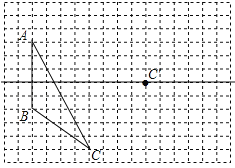
(1)请画出平移后的△A′B′C′;
(2)若连接AA′,CC′,则这两条线段之间的关系是 ;
(3)利用网格画出△ABC 中AC边上的中线BD;
(4)利用网格画出△ABC 中AB边上的高CE;
(5)△A′B′C′的面积为 .
【答案】(1)图解见解析;(2)平行且相等;(3)(4)图解见解析;(5)10;
【解析】
试题分析:(1)利用平移变换的性质得出对应点位置进而得出答案;
(2)利用平移变换的性质得出答案;
(3)利用网格结合三角形中线的性质得出答案;
(4)利用网格结合三角形高线的性质得出答案;
(5)利用平移的性质结合三角形面积求法得出答案.
解:(1)如图所示:△A′B′C′即为所求;
(2)连接AA′,CC′,则这两条线段之间的关系是平行且相等.
故答案为:平行且相等;
(3)如图所示:BD即为所求;
(4)如图所示:CE即为所求;
(5)△A′B′C′的面积为△ABC的面积:![]() ×5×4=10.
×5×4=10.
故答案为:10.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列判断不正确的是( )
A. 形状相同的图形是全等图形 B. 能够完全重合的两个三角形全等
C. 全等图形的形状和大小都相同 D. 全等三角形的对应角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索研究.请解决下列问题:
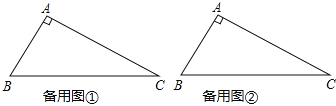
(1)已知△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,并把所有不同的分割方法都画出来,图不够可以自己画.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知等腰△ABC中,AB=AC,D为BC上一点,连接AD,若△ABD和△ACD都是等腰三角形,则∠B的度数为 (请画出示意图,并标明必要的角度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
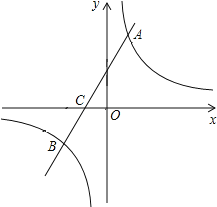
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接元旦小长假的购物高峰,黄兴南路步行街某运动品牌专卖店购进甲、乙两种服装,现此商店同时卖出甲、乙两种服装各一件,每件售价都为240元,其中一件赚了20%,另一件亏了20%,那么这个商店卖出这两件服装总体的盈亏情况是( )
A. 赚了12元 B. 亏了12元 C. 赚了20元 D. 亏了20元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
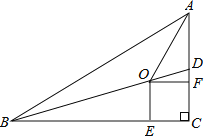
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
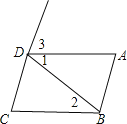
【题目】推理填空:如图:
①若∠1=∠2,
则 ∥ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 ∥ (同旁内角互补,两直线平行);
②当 ∥ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 ∥ 时,
∠3=∠C (两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
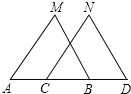
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com