
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
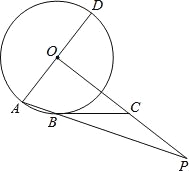
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
【答案】(1)证明见解析(2)7
【解析】
试题分析:(1)连结OB.由等腰三角形的性质得到∠A=∠OBA,∠P=∠CBP,由于OP⊥AD,得到∠A+∠P=90°,于是得到∠OBA+∠CBP=90°,求得∠OBC=90°结论可得;
(2)连结DB.由AD是⊙O的直径,得到∠ABD=90°,推出Rt△ABD∽Rt△AOP,得到比例式![]() ,即可得到结果.
,即可得到结果.
试题解析:(1)连结OB.
∵OA=OB,∴∠A=∠OBA,
又∵BC=PC,
∴∠P=∠CBP,
∵OP⊥AD,
∴∠A+∠P=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=180°﹣(∠OBA+∠CBP)=90°,
∵点B在⊙O上,
∴直线BC是⊙O的切线,
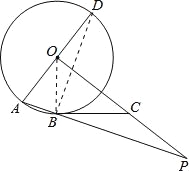
(2)如图,连结DB.
∵AD是⊙O的直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△AOP,
∴![]() ,即
,即![]() ,AP=9,
,AP=9,
∴BP=AP﹣BA=9﹣2=7.


科目:初中数学 来源: 题型:
【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
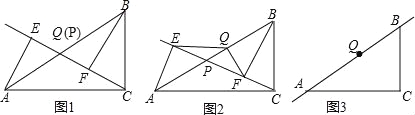
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.
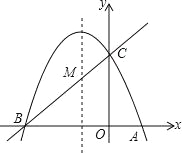
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列调查中,适宜采用普查的是( )
A.了解我省中学生的视力情况
B.了解八(1)班学生校服的尺码情况
C.检测一批炮弹的杀伤半径
D.调查电视剧《人民的名义》的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(3,-2)向下平移4个单位长度,得到点P的坐标为( )
A. (-1,-2) B. (3,-6) C. (7,-2) D. (3,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件是事件.(填“随机”或者“确定”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com