
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.
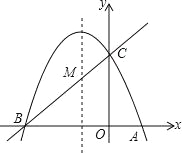
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
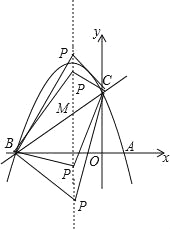
(2)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】(1)y=x+3, y=﹣x2﹣2x+3;(2)(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() ) 或(﹣1,
) 或(﹣1,![]() )
)
【解析】
试题分析:(1)首先由题意根据抛物线的对称性求得点B的坐标,然后利用交点式,求得抛物线的解析式;再利用待定系数法求得直线的解析式;
(2)首先利用勾股定理求得BC,PB,PC的长,然后分别从点B为直角顶点、点C为直角顶点、点P为直角顶点去分析求解即可求得答案.
试题解析:(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),抛物线与x轴的另一交点为B,
∴B的坐标为:(﹣3,0),
设抛物线的解析式为:y=a(x﹣1)(x+3),
把C(0,3)代入,﹣3a=3,
解得:a=﹣1,
∴抛物线的解析式为:y=﹣(x﹣1)(x+3)=﹣x2﹣2x+3;
把B(﹣3,0),C(0,3)代入y=mx+n得:
![]() ,
,
解得:![]() ,
,
∴直线y=mx+n的解析式为:y=x+3;
(2)设P(﹣1,t),
又∵B(﹣3,0),C(0,3),
∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,
①若点B为直角顶点,则BC2+PB2=PC2,
即:18+4+t2=t2﹣6t+10,解之得:t=﹣2;
②若点C为直角顶点,则BC2+PC2=PB2,
即:18+t2﹣6t+10=4+t2,解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2,
即:4+t2+t2﹣6t+10=18,
解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() ) 或(﹣1,
) 或(﹣1,![]() ).
).


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】|+2|=________,|-2|=________,-|-2|=________,-|+2|=________,|0|=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把点A(2,5)向下平移3个单位长度后,再向右平移2个单位长度,它的坐标是( )
A.(﹣1,5)
B.(2,2)
C.(4,2)
D.(﹣1,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
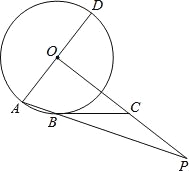
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有( )
A.6
B.5
C.4
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com