【题目】如图所示，在中，∠C＝90°，∠A＝30°．

（1）尺规作图：作线段AB的垂直平分线l（保留作图痕迹，不写作法）；

（2）在已作的图形中，若l分别交AB、AC及BC的延长线于点D、E、F，连接BE，求证：EF＝2DE．

参考答案：

【答案】（1）作图见解析；（2）证明见解析.

【解析】试题分析：

（1）分别以点A，B为圆心，以大于AB的一半为半径画圆，两圆交于两点，过这两点画直线，这条直线即是线段AB的垂直平分线；

（2）先证明ED=EC，再证∠F=30°，用含30°角的直角三角形的性质即可证明.

试题解析：

解：（1）如下图所示，直线l即为所求．

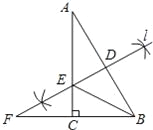
（2）证明：在Rt△ABC中，∵∠A＝30°，∠ABC＝60°，l为线段AB的垂直平分线，∴EA＝EB，∴∠EBA＝∠A=30°，∠AED＝∠BED=60°，

∴∠EBC＝30°＝∠EBA，∠FEC＝60°．

又∵ED⊥AB，EC⊥BC，∴ED＝EC．

在Rt△ECF中，∠FEC＝60°，∴∠EFC＝30°，∴EF＝2EC，∴EF＝2ED．

关闭