
【题目】小邢和小华相约放学后去公园跑步,她们一起以4km/h的速度从学校出发,走了15分钟后小邢发现忘了带作业,就以5km/h的速度回学校去拿,到达学校后,又用了6分钟取作业,之后便以同样的速度去追赶小华,结果在距公园3km处追上了小华,试求学校与公园的距离.
【答案】学校与公园的距离为14km.
【解析】
根据路程=速度×时间,计算出走了15分钟后,二者与学校的距离,根据时间=路程÷速度,计算出小邢返回学校所用的时间,两段时间相加,就是二者分开后小华走的时间,根据小华走的速度和时间,计算出二者分开后小华走的距离,设小邢追上小华所用的时间为th,根据二者的速度,时间,路程之间的关系,列出关于t的一元一次方程,解之,求出这段时间小华走的距离,四段距离之和即为学校与公园的距离,即可得到答案.
解:根据题意得:
走了15分钟后,二者与学校的距离为:4×![]() =1(km),
=1(km),
小邢返回学校所用的时间t1=![]() =0.2h,
=0.2h,
二者分开后小华走的时间为t2=0.2+![]() =0.3(h),
=0.3(h),
二者分开后小华走的距离为:4×0.3=1.2(km),
设小邢追上小华所用的时间为th,
根据题意得:
5t=4t+1+1.2,
解得:t=2.2,
这段时间小华走的距离为:4×2.2=8.8(km),
学校与公园的距离为:8.8+1+1.2+3=14(km),
答:学校与公园的距离为14km.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF.连结DE,过点E作EG⊥DE,使EG=DE,连结FG、FC
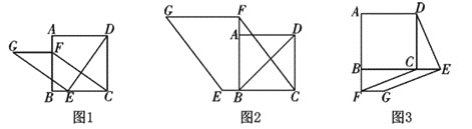
(1)请判断:FG与CE的数量关系是 ________,位置关系是________。
(2)如图2,若点E、F分别是边CB、BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E、F分别是边BC、AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,重庆仙女山风景区7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.2 | +0.4 | +0.8 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
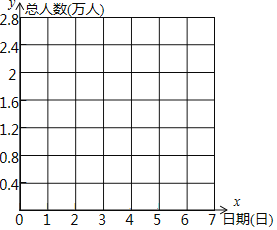
(1)若9月30日的游客人数记为a,请用含a的式子表示10月5日的游客人数: 万人.
(2)判断七天内游客人数最多的是 日,最少的是 日.
(3)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数情况:人数变化(万人)
查看答案和解析>>
科目:初中数学 来源: 题型:
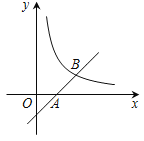
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() =
=![]() 的图象经过点A(1,0),与反比例函数
的图象经过点A(1,0),与反比例函数![]() =
=![]() (
(![]() >0)的图象相交于点B(2,1).
>0)的图象相交于点B(2,1).
(1)求![]() 的值和一次函数的解析式;
的值和一次函数的解析式;
(2)结合图象直接写出:当![]() >0时,不等式
>0时,不等式![]() >
>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
![]() “明天降雨的概率是
“明天降雨的概率是![]() ”表示明天有半天都在降雨;
”表示明天有半天都在降雨;
![]() 无理数是开方开不尽的数;
无理数是开方开不尽的数;
![]() 若
若![]() 为实数,则
为实数,则![]() 是不可能事件;
是不可能事件;
![]() 的平方根是
的平方根是![]() ,用式子表示是
,用式子表示是![]() ;
;
![]() 某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的教室A位于工地O的正西方向,且OA=200米,一部拖拉机从O点出发,以每秒5米的速度沿北偏西53°方向行驶,设拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机的噪声污染范围内,若不在,请说明理由;若在,求出教室A受污染的时间有几秒.(已知:sin53°≈0.80,sin37°≈0.60,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
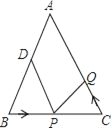
【题目】如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为_____ 厘米/秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
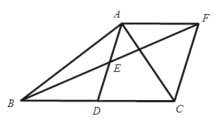
【题目】如图,在ABC 中, AD 是 BC 边上的中线,点 E 是 AD 的中点,过点 A 作AF // BC 交 BE 的延长线于 F ,连接CF .
(1)求证: AEF DEB ;
(2)若BAC 90,试判断四边形 ADCF 的形状,并证明你的结论;
(3)在(2)的情况下,如果 AC 2 ,点 M 在 AC 线段上移动,当 MB MD 有最小值时,求 AM 的长度(提示:以 D 点为原点, AD 为 y 正半轴, DC 为 x 正轴建立平面直角坐标系).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com