
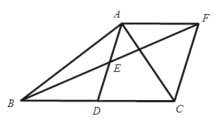
【题目】如图,在ABC 中, AD 是 BC 边上的中线,点 E 是 AD 的中点,过点 A 作AF // BC 交 BE 的延长线于 F ,连接CF .
(1)求证: AEF DEB ;
(2)若BAC 90,试判断四边形 ADCF 的形状,并证明你的结论;
(3)在(2)的情况下,如果 AC 2 ,点 M 在 AC 线段上移动,当 MB MD 有最小值时,求 AM 的长度(提示:以 D 点为原点, AD 为 y 正半轴, DC 为 x 正轴建立平面直角坐标系).
【答案】(1)证明见解析;(2)四边形ADCF是菱形;(3)![]() .
.
【解析】
(1)根据平行线的性质得到∠AFE=∠DBE,利用AAS定理证明△AEF≌△DEB;
(2)根据全等三角形的性质得到AF=DC,得到四边形ADCF是平行四边形,根据直角三角形的性质得到AD=DC,即可证明四边形ADCF是菱形;
(3)根据菱形的性质得到点D与点F关于直线AC对称,根据轴对称的性质作图即可得出点M,然后根据相似三角形的判定与性质即可得出AM与AC的关系,即可得出结论.
(1)∵AF∥BC,∴∠AFE=∠DBE.在△AEF和△DEB中,∵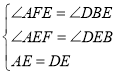 ,∴△AEF≌△DEB;
,∴△AEF≌△DEB;
(2)四边形ADCF是菱形,理由如下:
∵△AEF≌△DEB,∴AF=BD.
∵BD=DC,∴AF=DC.
又∵AF∥BC,∴四边形ADCF是平行四边形.
∵∠BAC=90°,AD是BC边上的中线,∴AD=DC,∴四边形ADCF是菱形;
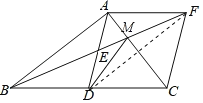
(3)连接BF交AC于M,则点M即为所求.
∵四边形ADCF是菱形,∴点D与点F关于直线AC对称,∴MD=MF,∴MB+MD=MB+MF=BF,即MB+MD有最小值.
∵AF=DC=BD,∴BC=2AF.
∵AF∥BC,∴△AMF∽△CMB,∴![]() ,∴
,∴![]() ,∴AM=
,∴AM=![]() AC.
AC.
∵AC=2,∴AM=![]() .
.


科目:初中数学 来源: 题型:
【题目】小邢和小华相约放学后去公园跑步,她们一起以4km/h的速度从学校出发,走了15分钟后小邢发现忘了带作业,就以5km/h的速度回学校去拿,到达学校后,又用了6分钟取作业,之后便以同样的速度去追赶小华,结果在距公园3km处追上了小华,试求学校与公园的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
查看答案和解析>>
科目:初中数学 来源: 题型:
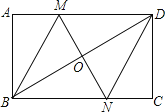
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
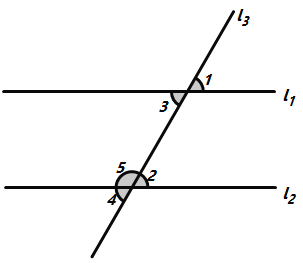
【题目】如图所示,直线![]() 、
、![]() 被
被![]() 所截:①命题“若
所截:①命题“若![]() ,则“
,则“![]() ”的题设是“
”的题设是“![]() ”,结论是“
”,结论是“![]() ”;②“若
”;②“若![]() ,则
,则![]() ”的依据是“两直线平行,同位角相等”;③“若
”的依据是“两直线平行,同位角相等”;③“若![]() ,则
,则![]() 不平行
不平行![]() ”的依据是“两直线平行,内错角相等”;④“若
”的依据是“两直线平行,内错角相等”;④“若![]() ,则
,则![]() ”依据是“两直线平行,同位角相等”;⑤“若
”依据是“两直线平行,同位角相等”;⑤“若![]() ,则
,则![]() ”的依据是“两直线平行,同旁内角互补”.上面说法正确的是(填序号)__________.
”的依据是“两直线平行,同旁内角互补”.上面说法正确的是(填序号)__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经营户,用![]() 元从菜农手里批发了长豆角和番茄共
元从菜农手里批发了长豆角和番茄共![]() 千克,长豆角和番茄当天的批发价和零售价如表:
千克,长豆角和番茄当天的批发价和零售价如表:
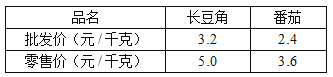
(1)这天该经营户批发了长豆角和番茄各多少千克?
(2)当天卖完这些番茄和长豆角能盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
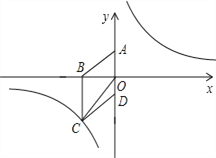
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且![]() (0,3)、
(0,3)、![]() (﹣4,0).
(﹣4,0).
(1)求经过点![]() 的反比例函数的解析式;
的反比例函数的解析式;
(2)设![]() 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以![]() 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com