
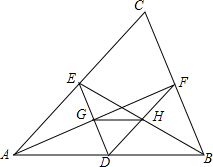
 如图所示,D为△ABC的边AB上的点,过D点作DE∥BC、DF∥AC,AF交DE于点G,BE交DF于点H,求证:GH∥AB.
如图所示,D为△ABC的边AB上的点,过D点作DE∥BC、DF∥AC,AF交DE于点G,BE交DF于点H,求证:GH∥AB. 分析 由题意可知四边形CEDF为平行四边形,从而可得到DE=CF,DF=EC,然后再证明△EDH∽△BFH,△AEG∽△FDG,利用相似三角形的性质和平行线分线段成比例定理可得到$\frac{DH}{HF}=\frac{AG}{GF}$,从而可证明$\frac{DF}{HF}=\frac{AF}{GF}$,故此△FGH∽△FAD,因而∠FGH=∠FAD,从而可证明:GH∥AD.
解答 解:∵ED∥CB,DF∥AC,
∴四边形CEDF为平行四边形.
∴DE=CF,DF=EC.
∵ED∥CB,
∴△EDH∽△BFH.
∴$\frac{DH}{HF}=\frac{DE}{FB}$.
∵DE=CF,
∴$\frac{DH}{HF}=\frac{CF}{FB}$.
又∵DF∥AC,
∴$\frac{CF}{FB}=\frac{AD}{DB}$.
∴$\frac{DH}{HF}=\frac{AD}{DB}$.
∵DF∥AE,
∴△AEG∽△FDG.
∴$\frac{AG}{GF}=\frac{AE}{DF}$.
∵DF=CE,
∴$\frac{AG}{GF}=\frac{AE}{CE}$.
又∵DE∥BC,
∴$\frac{AE}{CE}=\frac{AD}{DB}$.
∴$\frac{AG}{GF}=\frac{AD}{DB}$.
∴$\frac{DH}{HF}=\frac{AG}{GF}$.
∴$\frac{DH}{HF}+1=\frac{AG}{GF}+1$,即$\frac{DF}{HF}=\frac{AF}{GF}$.
又∵∠GFH=∠AFD,
∴△FGH∽△FAD.
∴∠FGH=∠FAD.
∴GH∥AD.
点评 本题主要考查的是相似三角形的性质和判定、平行线分线段成比例定理的应用,利用相似三角形的性质和平行线分线段成比例定理证得$\frac{DH}{HF}=\frac{AG}{GF}$是解题的关键.


科目:初中数学 来源: 题型:解答题
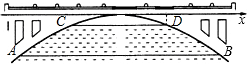 如图是一抛物线状拱桥,正常水位时,桥下的水面宽AB为20m,当水面上升3m到达警戒水位时,水面宽CD为10m
如图是一抛物线状拱桥,正常水位时,桥下的水面宽AB为20m,当水面上升3m到达警戒水位时,水面宽CD为10m查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx+4与函数y=$\frac{m}{x}$(x>0,m>0)的图象交于A、B两点,且与x、y轴分别交于C、D两点.
如图,直线y=kx+4与函数y=$\frac{m}{x}$(x>0,m>0)的图象交于A、B两点,且与x、y轴分别交于C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | h,t | B. | h,g | C. | t,g | D. | t |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
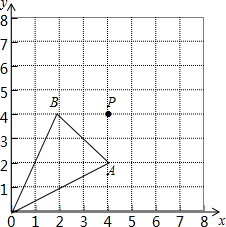 如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在网格中画出符合条件的△DEF.
如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在网格中画出符合条件的△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com