
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.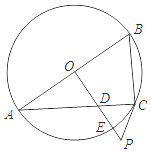
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
【答案】
(1)解:连接OC,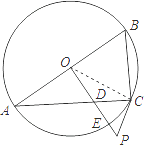
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCO+∠ACO=90°,
∵OC=OB,
∴∠B=∠BCO,
∵∠PCA=∠ABC,
∴∠BCO=∠ACP,
∴∠ACP+∠OCA=90°,
∴∠OCP=90°,
∴PC是⊙O的切线
(2)解:∵∠P=60°,PC=2,∠PCO=90°,
∴OC=2 ![]() ,OP=2PC=4,
,OP=2PC=4,
∴PE=OP﹣OE=OP﹣OC=4﹣2 ![]()
【解析】(1)连接OC,要证PC是⊙O的切线,只需证∠OCP=90°。根据直径所对的圆周角是直角可得∠ACB=90°,结合已知条件可证得∠OCP=90°,则结论可得。
(2)由(1)知∠PCO=90°,在直角三角形PCO中,根据直角三角形中,30度角所对的直角边等于斜边的一半可求出OP,则PE=OP﹣OE=OP﹣OC。


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 ![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是( )
A.10cm
B.30cm
C.60cm
D.50cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以4cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以3cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了 s时,以C点为圆心,2cm为半径的圆与直线EF相切.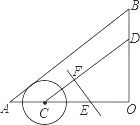
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页0.8元计费,但需按月付一定数额的承包费.两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
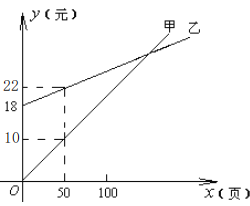
(1)乙复印社要求客户每月支付的承包费是_______元;
(2)当每月复印_______页时,两复印社实际收费相同;
(3)如果每月复印200页时,应选择_______复印社?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题:
(1)若OA顺时针转动,OB逆时针转动,t= 秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB= °;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是大于1的实数,且有a3+a-3=p,a3-a-3=q.
(1)若p+q=4,求p-q的值;
(2)当q2=22n+![]() -2(n≥1,且n是整数)时,比较p与a3+
-2(n≥1,且n是整数)时,比较p与a3+![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com