
【题目】如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是( )
A.10cm
B.30cm
C.60cm
D.50cm
科目:初中数学 来源: 题型:
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα= ![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ![]() ,求sin2β的值.
,求sin2β的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=2 ![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 . 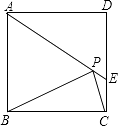
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.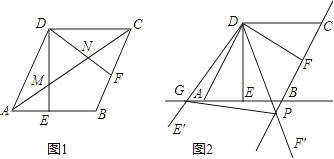
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN= ![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 ![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. A,B之间D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.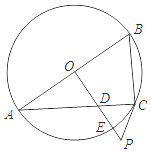
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简并求值
(1)5x2y+[7xy﹣2(3xy﹣2x2y)﹣xy],其中x=﹣1,y=﹣![]()
(2)已知a2﹣a﹣2=0,求a2﹣2(a2﹣a+3)﹣![]() (a2﹣a﹣4)的值.
(a2﹣a﹣4)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com