
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα= ![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
(1)【问题解决】
请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ= ![]() ,求sin2β的值.
,求sin2β的值.
【答案】
(1)解:如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα= ![]() ,可设BC=x,则AB=3x.
,可设BC=x,则AB=3x.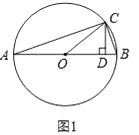
∴AC= ![]() =
= ![]() =2
=2 ![]() x,
x,
∵ ![]() ACBC=
ACBC= ![]() ABCD,
ABCD,
∴CD= ![]() x,
x,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠COB=2α,
∴sin2α= ![]() =
= ![]()
(2)解:如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.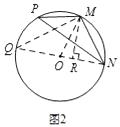
在⊙O中,∠NMQ=90°,
∵∠Q=∠P=β,∴∠MON=2∠Q=2β,
在Rt△QMN中,∵sinβ= ![]() ,
,
∴设MN=3k,则NQ=5k,易得OM= ![]() NQ=
NQ= ![]() ,
,
∴MQ= ![]() =4k,
=4k,
∵ ![]() ,
,
∴3k4k=5kMR
∴MR= ![]() ,
,
在Rt△MRO中,sin2β=sin∠MON= 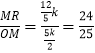 .
.
【解析】(1)通过圆周角定理构造2倍关系角和直角三角形,利用正弦定义可求出sin2α的值;(2)借鉴(1)的方法,通过圆周角定理把圆周角∠P转化为一条边过圆心的圆周角,进而构造出2倍角,利用定义求出正弦.


科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE. 
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.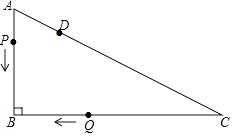
(1)点Q的速度为cm/s(用含x的代数式表示).
(2)求点P原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在 ![]() 中,
中, ![]() ,
, ![]() .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为 ![]() ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
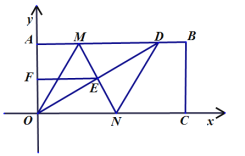
【题目】如图,在平面直角坐标系中,已知矩形AOCB的顶点O、A的坐标分别是(0,0)、(0,a),且满足![]() . 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
. 点D是AB上一点, M,N垂直平分OD,分别交AB,OD,OC于点M,E,N,连接OM,DN.
(1)填空:a = ;
(2)求证:四边形MOND是菱形;
(3)若F为OA的中点,连接EF,且满足EF+OE=9,求四边形MOND的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
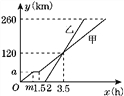
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 ![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是( )
A.10cm
B.30cm
C.60cm
D.50cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com